pax_global_header�����������������������������������������������������������������������������������0000666�0000000�0000000�00000000064�14455660762�0014531�g����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������52 comment=4ebcdbd412333893bd2674bc694924e21abf8915
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/���������������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0012677�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/�������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0014237�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/ISSUE_TEMPLATE/����������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0016422�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/ISSUE_TEMPLATE/bug_report.md���������������������������������������������������0000664�0000000�0000000�00000001066�14455660762�0021117�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������---
name: "Bug report"
about: Create a bug report to improve cmaes
title: ""
labels: bug
assignees: ''
---
# Bug reports
*Please file a bug report here.*
## Expected Behavior
*Please describe the behavior you are expecting*
## Current Behavior and Steps to Reproduce
*What is the current behavior? Please provide detailed steps or example for reproducing.*
## Context
Please provide any relevant information about your setup. This is important in case the issue is not reproducible except for under certain conditions.
* cmaes version or commit revision:
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/ISSUE_TEMPLATE/feature_request.md����������������������������������������������0000664�0000000�0000000�00000000271�14455660762�0022147�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������---
name: "Feature request"
about: Suggest an idea for new features in cmaes.
title: ""
labels: enhancement
assignees: ''
---
# Feature Request
*Please write your suggestion here.*
���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/workflows/���������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0016274�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/workflows/examples.yml���������������������������������������������������������0000664�0000000�0000000�00000003130�14455660762�0020632�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������name: Run examples
on:
pull_request:
paths:
- '.github/workflows/examples.yml'
- 'examples/**.py'
- 'cmaes/**.py'
jobs:
examples:
runs-on: ubuntu-latest
strategy:
matrix:
python-version: ["3.7", "3.8", "3.9", "3.10", "3.11"]
steps:
- uses: actions/checkout@v2
- name: Set up Python ${{ matrix.python-version }}
uses: actions/setup-python@v4
with:
python-version: ${{ matrix.python-version }}
architecture: x64
- name: Install dependencies
run: |
pip install -U pip setuptools
pip install --progress-bar off optuna numpy scipy
pip install --progress-bar off -U .
- run: python examples/quadratic_function.py
- run: python examples/ipop_cmaes.py
- run: python examples/bipop_cmaes.py
- run: python examples/ellipsoid_function.py
- run: python examples/optuna_sampler.py
- run: python examples/ws_cma_es.py
- run: python examples/cmaes_with_margin_binary.py
- run: python examples/cmaes_with_margin_integer.py
examples-cmawm-without-scipy:
runs-on: ubuntu-latest
steps:
- uses: actions/checkout@v2
- name: Set up Python
uses: actions/setup-python@v4
with:
python-version: 3.11
architecture: x64
check-latest: true
- name: Install dependencies
run: |
pip install -U pip setuptools
pip install --progress-bar off -U .
- run: python examples/cmaes_with_margin_binary.py
- run: python examples/cmaes_with_margin_integer.py
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/workflows/pypi-publish.yml�����������������������������������������������������0000664�0000000�0000000�00000002621�14455660762�0021445�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������name: Publish distributions to TestPyPI and PyPI
on:
push:
tags:
- v*.*.*
jobs:
build-n-publish:
name: Build and publish Python distributions to TestPyPI and PyPI
runs-on: ubuntu-latest
steps:
- uses: actions/checkout@v2
- name: Set up Python
uses: actions/setup-python@v4
with:
python-version: '3.x'
- name: Install dependencies
run: |
python -m pip install --upgrade pip setuptools
pip install --progress-bar off twine wheel
- name: Build distribution packages
run: python setup.py sdist bdist_wheel
- name: Verify the distributions
run: twine check dist/*
- uses: actions/upload-artifact@v2
with:
name: distribution
path: dist/
- name: Publish distribution to Test PyPI
uses: pypa/gh-action-pypi-publish@v1.4.1
with:
user: __token__
password: ${{ secrets.TEST_PYPI_PASSWORD }}
repository_url: https://test.pypi.org/legacy/
- name: Publish distribution to PyPI
uses: pypa/gh-action-pypi-publish@v1.4.1
with:
user: __token__
password: ${{ secrets.PYPI_PASSWORD }}
- name: Create GitHub release
env:
GITHUB_TOKEN: ${{ secrets.GITHUB_TOKEN }}
run: |
export TAGNAME=$(jq --raw-output .ref "$GITHUB_EVENT_PATH" | sed -e "s/refs\/tags\///")
gh release create ${TAGNAME} --draft dist/*
���������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.github/workflows/tests.yml������������������������������������������������������������0000664�0000000�0000000�00000002273�14455660762�0020165�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������name: Run tests and linters
on:
pull_request:
paths:
- '.github/workflows/tests.yml'
- 'pyproject.toml'
- '**.py'
jobs:
lint:
runs-on: ubuntu-latest
steps:
- uses: actions/checkout@v2
- name: Set up Python
uses: actions/setup-python@v4
with:
python-version: '3.x'
architecture: x64
- name: Install dependencies
run: |
python -m pip install --upgrade pip setuptools numpy
pip install --progress-bar off -r requirements-dev.txt
- run: flake8 . --show-source --statistics
- run: black --check .
- run: mypy cmaes
test:
runs-on: ubuntu-latest
strategy:
matrix:
python-version: ["3.7", "3.8", "3.9", "3.10", "3.11"]
steps:
- uses: actions/checkout@v2
- name: Setup Python${{ matrix.python-version }}
uses: actions/setup-python@v4
with:
python-version: ${{ matrix.python-version }}
architecture: x64
- name: Install dependencies
run: |
python -m pip install --upgrade pip setuptools numpy scipy hypothesis
pip install --progress-bar off .
- run: python -m unittest
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/.gitignore�����������������������������������������������������������������������������0000664�0000000�0000000�00000000174�14455660762�0014671�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������venv/
dist/
build/
__pycache__/
.mypy_cache/
*.pyc
.eggs/
*.egg-info/
.hypothesis
tmp/
benchmark/*.json
*.stats
*.sqlite3
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/LICENSE��������������������������������������������������������������������������������0000664�0000000�0000000�00000002066�14455660762�0013710�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������MIT License
Copyright (c) 2020-2021 CyberAgent, Inc.
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/README.md������������������������������������������������������������������������������0000664�0000000�0000000�00000040577�14455660762�0014173�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������# CMA-ES
[](./LICENSE) [](https://pypistats.org/packages/cmaes)
Lightweight Covariance Matrix Adaptation Evolution Strategy (CMA-ES) [1] implementation.

## News
* **2023/05/23** Our paper, [M. Nomura, Y. Akimoto, and I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?](https://arxiv.org/abs/2304.03473), has been nominated for the Best Paper Award in the ENUM track at GECCO'23 :whale:
* **2023/04/01** Two papers have been accepted to GECCO'23 ENUM Track: (1) [M. Nomura, Y. Akimoto, and I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?](https://arxiv.org/abs/2304.03473), and (2) [Y. Watanabe, K. Uchida, R. Hamano, S. Saito, M. Nomura, and S. Shirakawa, (1+1)-CMA-ES with Margin for Discrete and Mixed-Integer Problems](https://arxiv.org/abs/2305.00849) :tada:
* **2022/05/13** The paper, ["CMA-ES with Margin: Lower-Bounding Marginal Probability for Mixed-Integer Black-Box Optimization"](https://arxiv.org/abs/2205.13482) written by Hamano, Saito, [@nomuramasahir0](https://github.com/nomuramasahir0) (the maintainer of this library), and Shirakawa, has been nominated as best paper at GECCO'22 ENUM track.
* **2021/03/10** ["Introduction to CMA-ES sampler"](https://medium.com/optuna/introduction-to-cma-es-sampler-ee68194c8f88) is published at Optuna Medium Blog. This article explains when and how to make the best use out of CMA-ES sampler. Please check it out!
* **2021/02/02** The paper ["Warm Starting CMA-ES for Hyperparameter Optimization"](https://arxiv.org/abs/2012.06932) written by [@nomuramasahir0](https://github.com/nomuramasahir0), the maintainer of this library, is accepted at AAAI 2021 :tada:
* **2020/07/29** Optuna's built-in CMA-ES sampler which uses this library under the hood is stabled at Optuna v2.0. Please check out the [v2.0 release blog](https://medium.com/optuna/optuna-v2-3165e3f1fc2).
## Installation
Supported Python versions are 3.7 or later.
```
$ pip install cmaes
```
Or you can install via [conda-forge](https://anaconda.org/conda-forge/cmaes).
```
$ conda install -c conda-forge cmaes
```
## Usage
This library provides an "ask-and-tell" style interface.
```python
import numpy as np
from cmaes import CMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
```
And you can use this library via [Optuna](https://github.com/optuna/optuna) [2], an automatic hyperparameter optimization framework.
Optuna's built-in CMA-ES sampler which uses this library under the hood is available from [v1.3.0](https://github.com/optuna/optuna/releases/tag/v1.3.0) and stabled at [v2.0.0](https://github.com/optuna/optuna/releases/tag/v2.2.0).
See [the documentation](https://optuna.readthedocs.io/en/stable/reference/samplers/generated/optuna.samplers.CmaEsSampler.html) or [v2.0 release blog](https://medium.com/optuna/optuna-v2-3165e3f1fc2) for more details.
```python
import optuna
def objective(trial: optuna.Trial):
x1 = trial.suggest_uniform("x1", -4, 4)
x2 = trial.suggest_uniform("x2", -4, 4)
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
sampler = optuna.samplers.CmaEsSampler()
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=250)
```
## CMA-ES variants
#### CMA-ES with Margin [3]
CMA-ES with Margin introduces a lower bound on the marginal probability associated with each discrete dimension so that samples can avoid being fixed to a single point.
It can be applied to mixed spaces of continuous (float) and discrete (including integer and binary).
|CMA-ES|CMA-ESwM|
|---|---|
|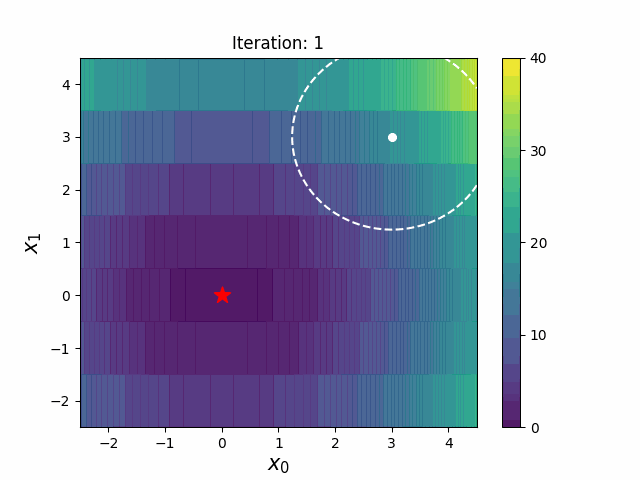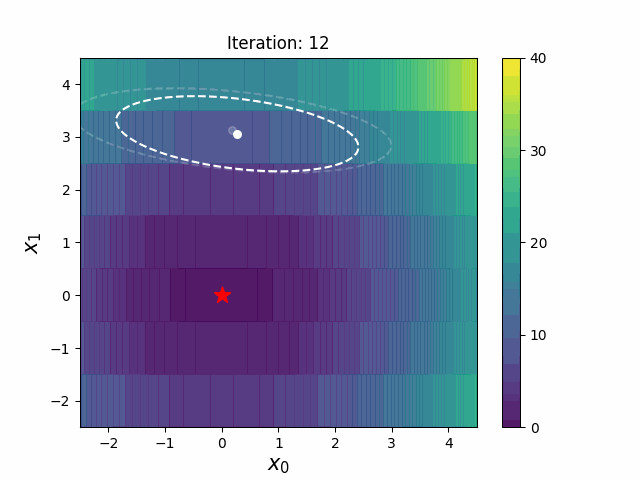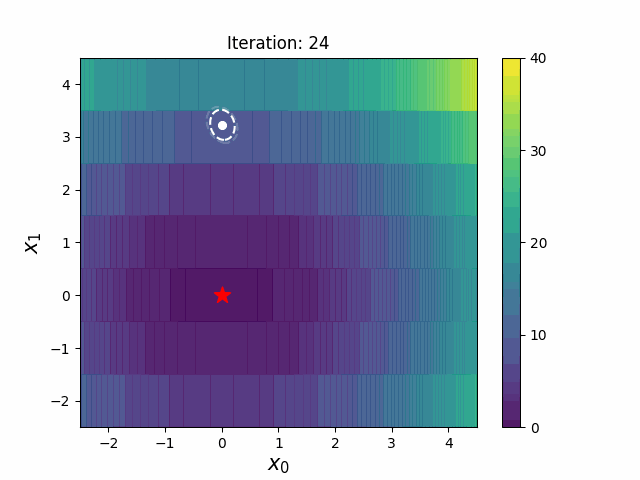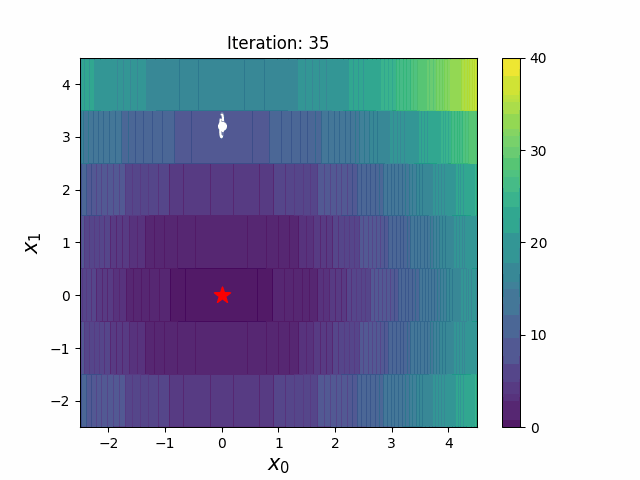||
The above figures are taken from [EvoConJP/CMA-ES_with_Margin](https://github.com/EvoConJP/CMA-ES_with_Margin).
Source code
```python
import numpy as np
from cmaes import CMAwM
def ellipsoid_onemax(x, n_zdim):
n = len(x)
n_rdim = n - n_zdim
r = 10
if len(x) < 2:
raise ValueError("dimension must be greater one")
ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
onemax = n_zdim - (0.0 < x[(n - n_zdim) :]).sum()
return ellipsoid + r * onemax
def main():
binary_dim, continuous_dim = 10, 10
dim = binary_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
np.tile([0, 1], (binary_dim, 1)),
]
)
steps = np.concatenate([np.zeros(continuous_dim), np.ones(binary_dim)])
optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_onemax(x_for_eval, binary_dim)
evals += 1
solutions.append((x_for_tell, value))
if evals % 300 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
```
Source code is also available [here](./examples/cmaes_with_margin.py).
#### Warm Starting CMA-ES [4]
Warm Starting CMA-ES is a method to transfer prior knowledge on similar HPO tasks through the initialization of CMA-ES.
Here is the result of an experiment that tuning LightGBM for Kaggle's Toxic Comment Classification Challenge data, a multilabel classification dataset.
In this benchmark, we use 10% of a full dataset as the source task, and a full dataset as the target task.
Please refer [the paper](https://arxiv.org/abs/2012.06932) and/or https://github.com/c-bata/benchmark-warm-starting-cmaes for more details of experiment settings.

Source code
```python
import numpy as np
from cmaes import CMA, get_warm_start_mgd
def source_task(x1: float, x2: float) -> float:
b = 0.4
return (x1 - b) ** 2 + (x2 - b) ** 2
def target_task(x1: float, x2: float) -> float:
b = 0.6
return (x1 - b) ** 2 + (x2 - b) ** 2
if __name__ == "__main__":
# Generate solutions from a source task
source_solutions = []
for _ in range(1000):
x = np.random.random(2)
value = source_task(x[0], x[1])
source_solutions.append((x, value))
# Estimate a promising distribution of the source task,
# then generate parameters of the multivariate gaussian distribution.
ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(
source_solutions, gamma=0.1, alpha=0.1
)
optimizer = CMA(mean=ws_mean, sigma=ws_sigma, cov=ws_cov)
# Run WS-CMA-ES
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = target_task(x[0], x[1])
solutions.append((x, value))
print(
f"{optimizer.generation:3d} {value:10.5f}"
f" {x[0]:6.2f} {x[1]:6.2f}"
)
optimizer.tell(solutions)
if optimizer.should_stop():
break
```
The full source code is available [here](./examples/ws_cma_es.py).
#### Separable CMA-ES [5]
sep-CMA-ES is an algorithm which constrains the covariance matrix to be diagonal.
Due to the reduction of the number of parameters, the learning rate for the covariance matrix can be increased.
Consequently, this algorithm outperforms CMA-ES on separable functions.
Source code
```python
import numpy as np
from cmaes import SepCMA
def ellipsoid(x):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
if __name__ == "__main__":
dim = 40
optimizer = SepCMA(mean=3 * np.ones(dim), sigma=2.0)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ellipsoid(x)
evals += 1
solutions.append((x, value))
if evals % 3000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
```
Full source code is available [here](./examples/sepcma_ellipsoid_function.py).
#### IPOP-CMA-ES [6]
IPOP-CMA-ES is a method to restart CMA-ES with increasing population size like below.

Source code
```python
import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
# https://www.sfu.ca/~ssurjano/ackley.html
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e + 20
)
if __name__ == "__main__":
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
if optimizer.should_stop():
# popsize multiplied by 2 (or 3) before each restart.
popsize = optimizer.population_size * 2
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(mean=mean, sigma=sigma, population_size=popsize)
print(f"Restart CMA-ES with popsize={popsize}")
```
Full source code is available [here](./examples/ipop_cmaes.py).
#### BIPOP-CMA-ES [7]
BIPOP-CMA-ES applies two interlaced restart strategies, one with an increasing population size and one with varying small population sizes.

Source code
```python
import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
# https://www.sfu.ca/~ssurjano/ackley.html
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e + 20
)
if __name__ == "__main__":
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
n_restarts = 0 # A small restart doesn't count in the n_restarts
small_n_eval, large_n_eval = 0, 0
popsize0 = optimizer.population_size
inc_popsize = 2
# Initial run is with "normal" population size; it is
# the large population before first doubling, but its
# budget accounting is the same as in case of small
# population.
poptype = "small"
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
if optimizer.should_stop():
n_eval = optimizer.population_size * optimizer.generation
if poptype == "small":
small_n_eval += n_eval
else: # poptype == "large"
large_n_eval += n_eval
if small_n_eval < large_n_eval:
poptype = "small"
popsize_multiplier = inc_popsize ** n_restarts
popsize = math.floor(
popsize0 * popsize_multiplier ** (np.random.uniform() ** 2)
)
else:
poptype = "large"
n_restarts += 1
popsize = popsize0 * (inc_popsize ** n_restarts)
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(
mean=mean,
sigma=sigma,
bounds=bounds,
population_size=popsize,
)
print("Restart CMA-ES with popsize={} ({})".format(popsize, poptype))
```
Full source code is available [here](./examples/bipop_cmaes.py).
## Benchmark results
| [Rosenbrock function](https://www.sfu.ca/~ssurjano/rosen.html) | [Six-Hump Camel function](https://www.sfu.ca/~ssurjano/camel6.html) |
| ------------------- | ----------------------- |
|  |  |
This implementation (green) stands comparison with [pycma](https://github.com/CMA-ES/pycma) (blue).
See [benchmark](./benchmark) for details.
## Links
**Projects using cmaes:**
* [Optuna](https://github.com/optuna/optuna) : A hyperparameter optimization framework that supports CMA-ES using this library under the hood.
* (If you have a project which uses `cmaes` and want your own project to be listed here, please submit a GitHub issue.)
**Other libraries:**
I respect all libraries involved in CMA-ES.
* [pycma](https://github.com/CMA-ES/pycma) : Most famous CMA-ES implementation by Nikolaus Hansen.
* [pymoo](https://github.com/msu-coinlab/pymoo) : Multi-objective optimization in Python.
* [evojax](https://github.com/google/evojax) : EvoJAX provides a JAX-port of this library.
* [evosax](https://github.com/RobertTLange/evosax) : evosax provides JAX-based CMA-ES and sep-CMA-ES implementation, which is inspired by this library.
**References:**
* [1] [N. Hansen, The CMA Evolution Strategy: A Tutorial. arXiv:1604.00772, 2016.](https://arxiv.org/abs/1604.00772)
* [2] [T. Akiba, S. Sano, T. Yanase, T. Ohta, M. Koyama, Optuna: A Next-generation Hyperparameter Optimization Framework, KDD, 2019.](https://dl.acm.org/citation.cfm?id=3330701)
* [3] [R. Hamano, S. Saito, M. Nomura, S. Shirakawa, CMA-ES with Margin: Lower-Bounding Marginal Probability for Mixed-Integer Black-Box Optimization, GECCO, 2022.](https://arxiv.org/abs/2205.13482)
* [4] [M. Nomura, S. Watanabe, Y. Akimoto, Y. Ozaki, M. Onishi, Warm Starting CMA-ES for Hyperparameter Optimization, AAAI, 2021.](https://arxiv.org/abs/2012.06932)
* [5] [R. Ros, N. Hansen, A Simple Modification in CMA-ES Achieving Linear Time and Space Complexity, PPSN, 2008.](https://hal.inria.fr/inria-00287367/document)
* [6] [A. Auger, N. Hansen, A restart CMA evolution strategy with increasing population size, CEC, 2005.](https://sci2s.ugr.es/sites/default/files/files/TematicWebSites/EAMHCO/contributionsCEC05/auger05ARCMA.pdf)
* [7] [N. Hansen, Benchmarking a BI-Population CMA-ES on the BBOB-2009 Function Testbed, GECCO Workshop, 2009.](https://hal.inria.fr/inria-00382093/document)
���������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/�����������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0014631�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/README.md��������������������������������������������������������������������0000664�0000000�0000000�00000003052�14455660762�0016110�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������# Continuous benchmarking using kurobako and GitHub Actions
Benchmark scripts are built on [kurobako](https://github.com/sile/kurobako).
See [Introduction to Kurobako: A Benchmark Tool for Hyperparameter Optimization Algorithms](https://medium.com/optuna/kurobako-a2e3f7b760c7) for more details.
## How to run benchmark scripts
GitHub Actions continuously run the benchmark scripts and comment on your pull request.
If you want to run on your local machines, please execute following after installed kurobako.
```console
$ ./benchmark/runner.sh -h
runner.sh is an entrypoint to run benchmarkers.
Usage:
$ runner.sh
Problem:
rosenbrock : https://www.sfu.ca/~ssurjano/rosen.html
six-hump-camel : https://www.sfu.ca/~ssurjano/camel6.html
himmelblau : https://en.wikipedia.org/wiki/Himmelblau%27s_function
ackley : https://www.sfu.ca/~ssurjano/ackley.html
rastrigin : https://www.sfu.ca/~ssurjano/rastr.html
Options:
--help, -h print this
Example:
$ runner.sh rosenbrock ./tmp/kurobako.json
$ cat ./tmp/kurobako.json | kurobako plot curve --errorbar -o ./tmp
$ ./benchmark/runner.sh rosenbrock ./tmp/kurobako.json
$ cat ./tmp/kurobako.json | kurobako plot curve --errorbar -o ./tmp
```
`kurobako plot curve` requires gnuplot. If you want to run on Docker container, please execute following:
```
$ docker pull sile/kurobako
$ ./benchmark/runner.sh rosenbrock ./tmp/kurobako.json
$ cat ./tmp/kurobako.json | docker run -v $PWD/tmp/images/:/images/ --rm -i sile/kurobako plot curve
```
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/optuna_solver.py�������������������������������������������������������������0000664�0000000�0000000�00000011633�14455660762�0020107�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import argparse
import optuna
import warnings
from kurobako import solver
from kurobako.solver.optuna import OptunaSolverFactory
warnings.filterwarnings(
"ignore",
category=optuna.exceptions.ExperimentalWarning,
module="optuna.samplers._cmaes",
)
parser = argparse.ArgumentParser()
parser.add_argument(
"sampler",
choices=["cmaes", "sep-cmaes", "ipop-cmaes", "ipop-sep-cmaes", "pycma", "ws-cmaes"],
)
parser.add_argument(
"--loglevel", choices=["debug", "info", "warning", "error"], default="warning"
)
parser.add_argument("--warm-starting-trials", type=int, default=0)
args = parser.parse_args()
if args.loglevel == "debug":
optuna.logging.set_verbosity(optuna.logging.DEBUG)
elif args.loglevel == "info":
optuna.logging.set_verbosity(optuna.logging.INFO)
elif args.loglevel == "warning":
optuna.logging.set_verbosity(optuna.logging.WARNING)
elif args.loglevel == "error":
optuna.logging.set_verbosity(optuna.logging.ERROR)
def create_cmaes_study(seed):
sampler = optuna.samplers.CmaEsSampler(seed=seed, warn_independent_sampling=True)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
def create_sep_cmaes_study(seed):
sampler = optuna.samplers.CmaEsSampler(
seed=seed, warn_independent_sampling=True, use_separable_cma=True
)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
def create_ipop_cmaes_study(seed):
sampler = optuna.samplers.CmaEsSampler(
seed=seed,
warn_independent_sampling=True,
restart_strategy="ipop",
inc_popsize=2,
)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
def create_ipop_sep_cmaes_study(seed):
sampler = optuna.samplers.CmaEsSampler(
seed=seed,
warn_independent_sampling=True,
restart_strategy="ipop",
inc_popsize=2,
use_separable_cma=True,
)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
def create_pycma_study(seed):
sampler = optuna.integration.PyCmaSampler(
seed=seed,
warn_independent_sampling=True,
)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
class WarmStartingCmaEsSampler(optuna.samplers.BaseSampler):
def __init__(self, seed, warm_starting_trials: int) -> None:
self._seed = seed
self._warm_starting = True
self._warm_starting_trials = warm_starting_trials
self._sampler = optuna.samplers.RandomSampler(seed=seed)
self._source_trials = []
def infer_relative_search_space(self, study, trial):
return self._sampler.infer_relative_search_space(study, trial)
def sample_relative(
self,
study,
trial,
search_space,
):
return self._sampler.sample_relative(study, trial, search_space)
def sample_independent(self, study, trial, param_name, param_distribution):
return self._sampler.sample_independent(
study, trial, param_name, param_distribution
)
def after_trial(
self,
study,
trial,
state,
values,
):
if not self._warm_starting:
return self._sampler.after_trial(study, trial, state, values)
if len(self._source_trials) < self._warm_starting_trials:
assert state == optuna.trial.TrialState.PRUNED
self._source_trials.append(
optuna.create_trial(
params=trial.params,
distributions=trial.distributions,
values=values,
)
)
if len(self._source_trials) == self._warm_starting_trials:
self._sampler = optuna.samplers.CmaEsSampler(
seed=self._seed + 1, source_trials=self._source_trials or None
)
self._warm_starting = False
else:
return self._sampler.after_trial(study, trial, state, values)
def create_warm_start_study(seed):
sampler = WarmStartingCmaEsSampler(seed, args.warm_starting_trials)
return optuna.create_study(sampler=sampler, pruner=optuna.pruners.NopPruner())
if __name__ == "__main__":
if args.sampler == "cmaes":
factory = OptunaSolverFactory(create_cmaes_study)
elif args.sampler == "sep-cmaes":
factory = OptunaSolverFactory(create_sep_cmaes_study)
elif args.sampler == "ipop-cmaes":
factory = OptunaSolverFactory(create_ipop_cmaes_study)
elif args.sampler == "ipop-sep-cmaes":
factory = OptunaSolverFactory(create_ipop_sep_cmaes_study)
elif args.sampler == "pycma":
factory = OptunaSolverFactory(create_pycma_study)
elif args.sampler == "ws-cmaes":
factory = OptunaSolverFactory(
create_warm_start_study, warm_starting_trials=args.warm_starting_trials
)
else:
raise ValueError("unsupported sampler")
runner = solver.SolverRunner(factory)
runner.run()
�����������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/problem_himmelblau.py��������������������������������������������������������0000664�0000000�0000000�00000002570�14455660762�0021046�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from kurobako import problem
from kurobako.problem import Problem
from typing import List
from typing import Optional
class HimmelblauEvaluator(problem.Evaluator):
def __init__(self, params: List[Optional[float]]):
self._x1, self._x2 = params
self._current_step = 0
def evaluate(self, next_step: int) -> List[float]:
self._current_step = 1
value = (self._x1**2 + self._x2 - 11.0) ** 2 + (
self._x1 + self._x2**2 - 7.0
) ** 2
return [value]
def current_step(self) -> int:
return self._current_step
class HimmelblauProblem(problem.Problem):
def create_evaluator(
self, params: List[Optional[float]]
) -> Optional[problem.Evaluator]:
return HimmelblauEvaluator(params)
class HimmelblauProblemFactory(problem.ProblemFactory):
def create_problem(self, seed: int) -> Problem:
return HimmelblauProblem()
def specification(self) -> problem.ProblemSpec:
params = [
problem.Var("x1", problem.ContinuousRange(-4, 4)),
problem.Var("x2", problem.ContinuousRange(-4, 4)),
]
return problem.ProblemSpec(
name="Himmelblau Function",
params=params,
values=[problem.Var("Himmelblau")],
)
if __name__ == "__main__":
runner = problem.ProblemRunner(HimmelblauProblemFactory())
runner.run()
����������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/problem_rastrigin.py���������������������������������������������������������0000664�0000000�0000000�00000003001�14455660762�0020717�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import sys
import numpy as np
from kurobako import problem
from kurobako.problem import Problem
from typing import List
from typing import Optional
class RastriginEvaluator(problem.Evaluator):
def __init__(self, params: List[Optional[float]]):
self.n = len(params)
self.x = np.array(params, dtype=float)
self._current_step = 0
def evaluate(self, next_step: int) -> List[float]:
self._current_step = 1
value = 10 * self.n + np.sum(self.x**2 - 10 * np.cos(2 * np.pi * self.x))
return [value]
def current_step(self) -> int:
return self._current_step
class RastriginProblem(problem.Problem):
def create_evaluator(
self, params: List[Optional[float]]
) -> Optional[problem.Evaluator]:
return RastriginEvaluator(params)
class RastriginProblemFactory(problem.ProblemFactory):
def __init__(self, dim):
self.dim = dim
def create_problem(self, seed: int) -> Problem:
return RastriginProblem()
def specification(self) -> problem.ProblemSpec:
params = [
problem.Var(f"x{i+1}", problem.ContinuousRange(-5.12, 5.12))
for i in range(self.dim)
]
return problem.ProblemSpec(
name=f"Rastrigin (dim={self.dim})",
params=params,
values=[problem.Var("Rastrigin")],
)
if __name__ == "__main__":
dim = int(sys.argv[1]) if len(sys.argv) == 2 else 2
runner = problem.ProblemRunner(RastriginProblemFactory(dim))
runner.run()
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/problem_rosenbrock.py��������������������������������������������������������0000664�0000000�0000000�00000002624�14455660762�0021076�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from kurobako import problem
from kurobako.problem import Problem
from typing import List
from typing import Optional
class RosenbrockEvaluator(problem.Evaluator):
"""
See https://www.sfu.ca/~ssurjano/rosen.html
"""
def __init__(self, params: List[Optional[float]]):
self._x1, self._x2 = params
self._current_step = 0
def evaluate(self, next_step: int) -> List[float]:
self._current_step = 1
value = 100 * (self._x2 - self._x1**2) ** 2 + (self._x1 - 1) ** 2
return [value]
def current_step(self) -> int:
return self._current_step
class RosenbrockProblem(problem.Problem):
def create_evaluator(
self, params: List[Optional[float]]
) -> Optional[problem.Evaluator]:
return RosenbrockEvaluator(params)
class RosenbrockProblemFactory(problem.ProblemFactory):
def create_problem(self, seed: int) -> Problem:
return RosenbrockProblem()
def specification(self) -> problem.ProblemSpec:
params = [
problem.Var("x1", problem.ContinuousRange(-5, 10)),
problem.Var("x2", problem.ContinuousRange(-5, 10)),
]
return problem.ProblemSpec(
name="Rosenbrock Function",
params=params,
values=[problem.Var("Rosenbrock")],
)
if __name__ == "__main__":
runner = problem.ProblemRunner(RosenbrockProblemFactory())
runner.run()
������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/problem_six_hump_camel.py����������������������������������������������������0000664�0000000�0000000�00000003034�14455660762�0021720�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from kurobako import problem
from kurobako.problem import Problem
from typing import List
from typing import Optional
class SixHumpCamelEvaluator(problem.Evaluator):
"""
See https://www.sfu.ca/~ssurjano/camel6.html
"""
def __init__(self, params: List[Optional[float]]):
self._x1, self._x2 = params
self._current_step = 0
def evaluate(self, next_step: int) -> List[float]:
self._current_step = 1
value = (
(4 - 2.1 * (self._x1**2) + (self._x1**4) / 3) * (self._x1**2)
+ self._x1 * self._x2
+ (-4 + 4 * self._x2**2) * (self._x2**2)
)
return [value]
def current_step(self) -> int:
return self._current_step
class SixHumpCamelProblem(problem.Problem):
def create_evaluator(
self, params: List[Optional[float]]
) -> Optional[problem.Evaluator]:
return SixHumpCamelEvaluator(params)
class SixHumpCamelProblemFactory(problem.ProblemFactory):
def create_problem(self, seed: int) -> Problem:
return SixHumpCamelProblem()
def specification(self) -> problem.ProblemSpec:
params = [
problem.Var("x1", problem.ContinuousRange(-5, 10)),
problem.Var("x2", problem.ContinuousRange(-5, 10)),
]
return problem.ProblemSpec(
name="Six-Hump Camel Function",
params=params,
values=[problem.Var("Six-Hump Camel")],
)
if __name__ == "__main__":
runner = problem.ProblemRunner(SixHumpCamelProblemFactory())
runner.run()
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/benchmark/runner.sh��������������������������������������������������������������������0000775�0000000�0000000�00000006545�14455660762�0016513�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������#!/bin/sh
set -e
KUROBAKO=${KUROBAKO:-kurobako}
DIR=$(cd $(dirname $0); pwd)
REPEATS=${REPEATS:-5}
BUDGET=${BUDGET:-300}
SEED=${SEED:-1}
DIM=${DIM:-2}
SURROGATE_ROOT=${SURROGATE_ROOT:-$(dirname $DIR)/tmp/surrogate-models}
WARM_START=${WARM_START:-0}
usage() {
cat <
Problem:
rosenbrock : https://www.sfu.ca/~ssurjano/rosen.html
six-hump-camel : https://www.sfu.ca/~ssurjano/camel6.html
himmelblau : https://en.wikipedia.org/wiki/Himmelblau%27s_function
ackley : https://www.sfu.ca/~ssurjano/ackley.html
rastrigin : https://www.sfu.ca/~ssurjano/rastr.html
toxic-lightgbm : https://github.com/c-bata/benchmark-warm-starting-cmaes
Options:
--help, -h print this
Example:
$ $(basename ${0}) rosenbrock ./tmp/kurobako.json
$ cat ./tmp/kurobako.json | kurobako plot curve --errorbar -o ./tmp
EOF
}
case "$1" in
himmelblau)
PROBLEM=$($KUROBAKO problem command python $DIR/problem_himmelblau.py)
;;
rosenbrock)
PROBLEM=$($KUROBAKO problem command python $DIR/problem_rosenbrock.py)
;;
six-hump-camel)
PROBLEM=$($KUROBAKO problem command python $DIR/problem_six_hump_camel.py)
;;
ackley)
PROBLEM=$($KUROBAKO problem sigopt --dim $DIM ackley)
;;
rastrigin)
# "kurobako problem sigopt --dim 8 rastrigin" only accepts 8-dim.
PROBLEM=$($KUROBAKO problem command python $DIR/problem_rastrigin.py $DIM)
;;
toxic-lightgbm)
PROBLEM=$($KUROBAKO problem warm-starting \
$($KUROBAKO problem surrogate $SURROGATE_ROOT/wscmaes-toxic-source/) \
$($KUROBAKO problem surrogate $SURROGATE_ROOT/wscmaes-toxic-target/))
;;
help|--help|-h)
usage
exit 0
;;
*)
echo "[Error] Invalid problem '${1}'"
usage
exit 1
;;
esac
RANDOM_SOLVER=$($KUROBAKO solver random)
CMAES_SOLVER=$($KUROBAKO solver --name 'cmaes' command -- python $DIR/optuna_solver.py cmaes)
SEP_CMAES_SOLVER=$($KUROBAKO solver --name 'sep-cmaes' command -- python $DIR/optuna_solver.py sep-cmaes)
IPOP_CMAES_SOLVER=$($KUROBAKO solver --name 'ipop-cmaes' command -- python $DIR/optuna_solver.py ipop-cmaes)
IPOP_SEP_CMAES_SOLVER=$($KUROBAKO solver --name 'ipop-sep-cmaes' command -- python $DIR/optuna_solver.py ipop-sep-cmaes)
PYCMA_SOLVER=$($KUROBAKO solver --name 'pycma' command -- python $DIR/optuna_solver.py pycma)
WS_CMAES_SOLVER=$($KUROBAKO solver --name 'ws-cmaes' command -- python $DIR/optuna_solver.py ws-cmaes --warm-starting-trials $WARM_START)
if [ $WARM_START -gt 0 ]; then
$KUROBAKO studies \
--solvers $CMAES_SOLVER $WS_CMAES_SOLVER \
--problems $PROBLEM \
--seed $SEED --repeats $REPEATS --budget $BUDGET \
| $KUROBAKO run --parallelism 6 > $2
elif [ $BUDGET -le 500 ]; then
$KUROBAKO studies \
--solvers $RANDOM_SOLVER $PYCMA_SOLVER $CMAES_SOLVER $SEP_CMAES_SOLVER \
--problems $PROBLEM \
--seed $SEED --repeats $REPEATS --budget $BUDGET \
| $KUROBAKO run --parallelism 4 > $2
else
$KUROBAKO studies \
--solvers $RANDOM_SOLVER $CMAES_SOLVER $IPOP_SEP_CMAES_SOLVER $IPOP_CMAES_SOLVER $SEP_CMAES_SOLVER \
--problems $PROBLEM \
--seed $SEED --repeats $REPEATS --budget $BUDGET \
| $KUROBAKO run --parallelism 6 > $2
fi
�����������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/���������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0013767�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/__init__.py����������������������������������������������������������������������0000664�0000000�0000000�00000000366�14455660762�0016105�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from ._cma import CMA # NOQA
from ._sepcma import SepCMA # NOQA
from ._warm_start import get_warm_start_mgd # NOQA
from ._cmawm import CMAwM # NOQA
from ._xnes import XNES # NOQA
from ._dxnesic import DXNESIC # NOQA
__version__ = "0.10.0"
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/_cma.py��������������������������������������������������������������������������0000664�0000000�0000000�00000044764�14455660762�0015257�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import math
import numpy as np
from typing import Any
from typing import cast
from typing import Optional
_EPS = 1e-8
_MEAN_MAX = 1e32
_SIGMA_MAX = 1e32
class CMA:
"""CMA-ES stochastic optimizer class with ask-and-tell interface.
Example:
.. code::
import numpy as np
from cmaes import CMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
# Tell evaluation values.
optimizer.tell(solutions)
Args:
mean:
Initial mean vector of multi-variate gaussian distributions.
sigma:
Initial standard deviation of covariance matrix.
bounds:
Lower and upper domain boundaries for each parameter (optional).
n_max_resampling:
A maximum number of resampling parameters (default: 100).
If all sampled parameters are infeasible, the last sampled one
will be clipped with lower and upper bounds.
seed:
A seed number (optional).
population_size:
A population size (optional).
cov:
A covariance matrix (optional).
lr_adapt:
Flag for learning rate adaptation (optional; default=False)
"""
def __init__(
self,
mean: np.ndarray,
sigma: float,
bounds: Optional[np.ndarray] = None,
n_max_resampling: int = 100,
seed: Optional[int] = None,
population_size: Optional[int] = None,
cov: Optional[np.ndarray] = None,
lr_adapt: bool = False,
):
assert sigma > 0, "sigma must be non-zero positive value"
assert np.all(
np.abs(mean) < _MEAN_MAX
), f"Abs of all elements of mean vector must be less than {_MEAN_MAX}"
n_dim = len(mean)
assert n_dim > 1, "The dimension of mean must be larger than 1"
if population_size is None:
population_size = 4 + math.floor(3 * math.log(n_dim)) # (eq. 48)
assert population_size > 0, "popsize must be non-zero positive value."
mu = population_size // 2
# (eq.49)
weights_prime = np.array(
[
math.log((population_size + 1) / 2) - math.log(i + 1)
for i in range(population_size)
]
)
mu_eff = (np.sum(weights_prime[:mu]) ** 2) / np.sum(weights_prime[:mu] ** 2)
mu_eff_minus = (np.sum(weights_prime[mu:]) ** 2) / np.sum(
weights_prime[mu:] ** 2
)
# learning rate for the rank-one update
alpha_cov = 2
c1 = alpha_cov / ((n_dim + 1.3) ** 2 + mu_eff)
# learning rate for the rank-μ update
cmu = min(
1 - c1 - 1e-8, # 1e-8 is for large popsize.
alpha_cov
* (mu_eff - 2 + 1 / mu_eff)
/ ((n_dim + 2) ** 2 + alpha_cov * mu_eff / 2),
)
assert c1 <= 1 - cmu, "invalid learning rate for the rank-one update"
assert cmu <= 1 - c1, "invalid learning rate for the rank-μ update"
min_alpha = min(
1 + c1 / cmu, # eq.50
1 + (2 * mu_eff_minus) / (mu_eff + 2), # eq.51
(1 - c1 - cmu) / (n_dim * cmu), # eq.52
)
# (eq.53)
positive_sum = np.sum(weights_prime[weights_prime > 0])
negative_sum = np.sum(np.abs(weights_prime[weights_prime < 0]))
weights = np.where(
weights_prime >= 0,
1 / positive_sum * weights_prime,
min_alpha / negative_sum * weights_prime,
)
cm = 1 # (eq. 54)
# learning rate for the cumulation for the step-size control (eq.55)
c_sigma = (mu_eff + 2) / (n_dim + mu_eff + 5)
d_sigma = 1 + 2 * max(0, math.sqrt((mu_eff - 1) / (n_dim + 1)) - 1) + c_sigma
assert (
c_sigma < 1
), "invalid learning rate for cumulation for the step-size control"
# learning rate for cumulation for the rank-one update (eq.56)
cc = (4 + mu_eff / n_dim) / (n_dim + 4 + 2 * mu_eff / n_dim)
assert cc <= 1, "invalid learning rate for cumulation for the rank-one update"
self._n_dim = n_dim
self._popsize = population_size
self._mu = mu
self._mu_eff = mu_eff
self._cc = cc
self._c1 = c1
self._cmu = cmu
self._c_sigma = c_sigma
self._d_sigma = d_sigma
self._cm = cm
# E||N(0, I)|| (p.28)
self._chi_n = math.sqrt(self._n_dim) * (
1.0 - (1.0 / (4.0 * self._n_dim)) + 1.0 / (21.0 * (self._n_dim**2))
)
self._weights = weights
# evolution path
self._p_sigma = np.zeros(n_dim)
self._pc = np.zeros(n_dim)
self._mean = mean.copy()
if cov is None:
self._C = np.eye(n_dim)
else:
assert cov.shape == (n_dim, n_dim), "Invalid shape of covariance matrix"
self._C = cov
self._sigma = sigma
self._D: Optional[np.ndarray] = None
self._B: Optional[np.ndarray] = None
# bounds contains low and high of each parameter.
assert bounds is None or _is_valid_bounds(bounds, mean), "invalid bounds"
self._bounds = bounds
self._n_max_resampling = n_max_resampling
self._g = 0
self._rng = np.random.RandomState(seed)
# for learning rate adaptation
self._lr_adapt = lr_adapt
self._alpha = 1.4
self._beta_mean = 0.1
self._beta_Sigma = 0.03
self._gamma = 0.1
self._Emean = np.zeros([self._n_dim, 1])
self._ESigma = np.zeros([self._n_dim * self._n_dim, 1])
self._Vmean = 0.0
self._VSigma = 0.0
self._eta_mean = 1.0
self._eta_Sigma = 1.0
# Termination criteria
self._tolx = 1e-12 * sigma
self._tolxup = 1e4
self._tolfun = 1e-12
self._tolconditioncov = 1e14
self._funhist_term = 10 + math.ceil(30 * n_dim / population_size)
self._funhist_values = np.empty(self._funhist_term * 2)
def __getstate__(self) -> dict[str, Any]:
attrs = {}
for name in self.__dict__:
# Remove _rng in pickle serialized object.
if name == "_rng":
continue
if name == "_C":
sym1d = _compress_symmetric(self._C)
attrs["_c_1d"] = sym1d
continue
attrs[name] = getattr(self, name)
return attrs
def __setstate__(self, state: dict[str, Any]) -> None:
state["_C"] = _decompress_symmetric(state["_c_1d"])
del state["_c_1d"]
self.__dict__.update(state)
# Set _rng for unpickled object.
setattr(self, "_rng", np.random.RandomState())
@property
def dim(self) -> int:
"""A number of dimensions"""
return self._n_dim
@property
def population_size(self) -> int:
"""A population size"""
return self._popsize
@property
def generation(self) -> int:
"""Generation number which is monotonically incremented
when multi-variate gaussian distribution is updated."""
return self._g
def reseed_rng(self, seed: int) -> None:
self._rng.seed(seed)
def set_bounds(self, bounds: Optional[np.ndarray]) -> None:
"""Update boundary constraints"""
assert bounds is None or _is_valid_bounds(bounds, self._mean), "invalid bounds"
self._bounds = bounds
def ask(self) -> np.ndarray:
"""Sample a parameter"""
for i in range(self._n_max_resampling):
x = self._sample_solution()
if self._is_feasible(x):
return x
x = self._sample_solution()
x = self._repair_infeasible_params(x)
return x
def _eigen_decomposition(self) -> tuple[np.ndarray, np.ndarray]:
if self._B is not None and self._D is not None:
return self._B, self._D
self._C = (self._C + self._C.T) / 2
D2, B = np.linalg.eigh(self._C)
D = np.sqrt(np.where(D2 < 0, _EPS, D2))
self._C = np.dot(np.dot(B, np.diag(D**2)), B.T)
self._B, self._D = B, D
return B, D
def _sample_solution(self) -> np.ndarray:
B, D = self._eigen_decomposition()
z = self._rng.randn(self._n_dim) # ~ N(0, I)
y = cast(np.ndarray, B.dot(np.diag(D))).dot(z) # ~ N(0, C)
x = self._mean + self._sigma * y # ~ N(m, σ^2 C)
return x
def _is_feasible(self, param: np.ndarray) -> bool:
if self._bounds is None:
return True
return cast(
bool,
np.all(param >= self._bounds[:, 0]) and np.all(param <= self._bounds[:, 1]),
) # Cast bool_ to bool.
def _repair_infeasible_params(self, param: np.ndarray) -> np.ndarray:
if self._bounds is None:
return param
# clip with lower and upper bound.
param = np.where(param < self._bounds[:, 0], self._bounds[:, 0], param)
param = np.where(param > self._bounds[:, 1], self._bounds[:, 1], param)
return param
def tell(self, solutions: list[tuple[np.ndarray, float]]) -> None:
"""Tell evaluation values"""
assert len(solutions) == self._popsize, "Must tell popsize-length solutions."
for s in solutions:
assert np.all(
np.abs(s[0]) < _MEAN_MAX
), f"Abs of all param values must be less than {_MEAN_MAX} to avoid overflow errors"
self._g += 1
solutions.sort(key=lambda s: s[1])
# Stores 'best' and 'worst' values of the
# last 'self._funhist_term' generations.
funhist_idx = 2 * (self.generation % self._funhist_term)
self._funhist_values[funhist_idx] = solutions[0][1]
self._funhist_values[funhist_idx + 1] = solutions[-1][1]
# Sample new population of search_points, for k=1, ..., popsize
B, D = self._eigen_decomposition()
self._B, self._D = None, None
# keep old values for learning rate adaptation
if self._lr_adapt:
old_mean = np.copy(self._mean)
old_sigma = self._sigma
old_Sigma = self._sigma**2 * self._C
old_invsqrtC = B @ np.diag(1 / D) @ B.T
else:
old_mean, old_sigma, old_Sigma, old_invsqrtC = None, None, None, None
x_k = np.array([s[0] for s in solutions]) # ~ N(m, σ^2 C)
y_k = (x_k - self._mean) / self._sigma # ~ N(0, C)
# Selection and recombination
y_w = np.sum(y_k[: self._mu].T * self._weights[: self._mu], axis=1) # eq.41
self._mean += self._cm * self._sigma * y_w
# Step-size control
C_2 = cast(
np.ndarray, cast(np.ndarray, B.dot(np.diag(1 / D))).dot(B.T)
) # C^(-1/2) = B D^(-1) B^T
self._p_sigma = (1 - self._c_sigma) * self._p_sigma + math.sqrt(
self._c_sigma * (2 - self._c_sigma) * self._mu_eff
) * C_2.dot(y_w)
norm_p_sigma = np.linalg.norm(self._p_sigma)
self._sigma *= np.exp(
(self._c_sigma / self._d_sigma) * (norm_p_sigma / self._chi_n - 1)
)
self._sigma = min(self._sigma, _SIGMA_MAX)
# Covariance matrix adaption
h_sigma_cond_left = norm_p_sigma / math.sqrt(
1 - (1 - self._c_sigma) ** (2 * (self._g + 1))
)
h_sigma_cond_right = (1.4 + 2 / (self._n_dim + 1)) * self._chi_n
h_sigma = 1.0 if h_sigma_cond_left < h_sigma_cond_right else 0.0 # (p.28)
# (eq.45)
self._pc = (1 - self._cc) * self._pc + h_sigma * math.sqrt(
self._cc * (2 - self._cc) * self._mu_eff
) * y_w
# (eq.46)
w_io = self._weights * np.where(
self._weights >= 0,
1,
self._n_dim / (np.linalg.norm(C_2.dot(y_k.T), axis=0) ** 2 + _EPS),
)
delta_h_sigma = (1 - h_sigma) * self._cc * (2 - self._cc) # (p.28)
assert delta_h_sigma <= 1
# (eq.47)
rank_one = np.outer(self._pc, self._pc)
rank_mu = np.sum(
np.array([w * np.outer(y, y) for w, y in zip(w_io, y_k)]), axis=0
)
self._C = (
(
1
+ self._c1 * delta_h_sigma
- self._c1
- self._cmu * np.sum(self._weights)
)
* self._C
+ self._c1 * rank_one
+ self._cmu * rank_mu
)
# Learning rate adaptation: https://arxiv.org/abs/2304.03473
if self._lr_adapt:
assert isinstance(old_mean, np.ndarray)
assert isinstance(old_sigma, float)
assert isinstance(old_Sigma, np.ndarray)
assert isinstance(old_invsqrtC, np.ndarray)
self._lr_adaptation(old_mean, old_sigma, old_Sigma, old_invsqrtC)
def _lr_adaptation(
self,
old_mean: np.ndarray,
old_sigma: float,
old_Sigma: np.ndarray,
old_invsqrtC: np.ndarray,
) -> None:
# calculate one-step difference of the parameters
Deltamean = (self._mean - old_mean).reshape([self._n_dim, 1])
Sigma = (self._sigma**2) * self._C
# note that we use here matrix representation instead of vec one
DeltaSigma = Sigma - old_Sigma
# local coordinate
old_inv_sqrtSigma = old_invsqrtC / old_sigma
locDeltamean = old_inv_sqrtSigma.dot(Deltamean)
locDeltaSigma = (
old_inv_sqrtSigma.dot(DeltaSigma.dot(old_inv_sqrtSigma))
).reshape(self.dim * self.dim, 1) / np.sqrt(2)
# moving average E and V
self._Emean = (
1 - self._beta_mean
) * self._Emean + self._beta_mean * locDeltamean
self._ESigma = (
1 - self._beta_Sigma
) * self._ESigma + self._beta_Sigma * locDeltaSigma
self._Vmean = (1 - self._beta_mean) * self._Vmean + self._beta_mean * (
float(np.linalg.norm(locDeltamean)) ** 2
)
self._VSigma = (1 - self._beta_Sigma) * self._VSigma + self._beta_Sigma * (
float(np.linalg.norm(locDeltaSigma)) ** 2
)
# estimate SNR
sqnormEmean = np.linalg.norm(self._Emean) ** 2
hatSNRmean = (
sqnormEmean - (self._beta_mean / (2 - self._beta_mean)) * self._Vmean
) / (self._Vmean - sqnormEmean)
sqnormESigma = np.linalg.norm(self._ESigma) ** 2
hatSNRSigma = (
sqnormESigma - (self._beta_Sigma / (2 - self._beta_Sigma)) * self._VSigma
) / (self._VSigma - sqnormESigma)
# update learning rate
before_eta_mean = self._eta_mean
relativeSNRmean = np.clip(
(hatSNRmean / self._alpha / self._eta_mean) - 1, -1, 1
)
self._eta_mean = self._eta_mean * np.exp(
min(self._gamma * self._eta_mean, self._beta_mean) * relativeSNRmean
)
relativeSNRSigma = np.clip(
(hatSNRSigma / self._alpha / self._eta_Sigma) - 1, -1, 1
)
self._eta_Sigma = self._eta_Sigma * np.exp(
min(self._gamma * self._eta_Sigma, self._beta_Sigma) * relativeSNRSigma
)
# cap
self._eta_mean = min(self._eta_mean, 1.0)
self._eta_Sigma = min(self._eta_Sigma, 1.0)
# update parameters
self._mean = old_mean + self._eta_mean * Deltamean.reshape(self._n_dim)
Sigma = old_Sigma + self._eta_Sigma * DeltaSigma
# decompose Sigma to sigma and C
eigs, _ = np.linalg.eigh(Sigma)
logeigsum = sum([np.log(e) for e in eigs])
self._sigma = np.exp(logeigsum / 2.0 / self._n_dim)
self._sigma = min(self._sigma, _SIGMA_MAX)
self._C = Sigma / (self._sigma**2)
# step-size correction
self._sigma *= before_eta_mean / self._eta_mean
def should_stop(self) -> bool:
B, D = self._eigen_decomposition()
dC = np.diag(self._C)
# Stop if the range of function values of the recent generation is below tolfun.
if (
self.generation > self._funhist_term
and np.max(self._funhist_values) - np.min(self._funhist_values)
< self._tolfun
):
return True
# Stop if the std of the normal distribution is smaller than tolx
# in all coordinates and pc is smaller than tolx in all components.
if np.all(self._sigma * dC < self._tolx) and np.all(
self._sigma * self._pc < self._tolx
):
return True
# Stop if detecting divergent behavior.
if self._sigma * np.max(D) > self._tolxup:
return True
# No effect coordinates: stop if adding 0.2-standard deviations
# in any single coordinate does not change m.
if np.any(self._mean == self._mean + (0.2 * self._sigma * np.sqrt(dC))):
return True
# No effect axis: stop if adding 0.1-standard deviation vector in
# any principal axis direction of C does not change m. "pycma" check
# axis one by one at each generation.
i = self.generation % self.dim
if np.all(self._mean == self._mean + (0.1 * self._sigma * D[i] * B[:, i])):
return True
# Stop if the condition number of the covariance matrix exceeds 1e14.
condition_cov = np.max(D) / np.min(D)
if condition_cov > self._tolconditioncov:
return True
return False
def _is_valid_bounds(bounds: Optional[np.ndarray], mean: np.ndarray) -> bool:
if bounds is None:
return True
if (mean.size, 2) != bounds.shape:
return False
if not np.all(bounds[:, 0] <= mean):
return False
if not np.all(mean <= bounds[:, 1]):
return False
return True
def _compress_symmetric(sym2d: np.ndarray) -> np.ndarray:
assert len(sym2d.shape) == 2 and sym2d.shape[0] == sym2d.shape[1]
n = sym2d.shape[0]
dim = (n * (n + 1)) // 2
sym1d = np.zeros(dim)
start = 0
for i in range(n):
sym1d[start : start + n - i] = sym2d[i][i:] # noqa: E203
start += n - i
return sym1d
def _decompress_symmetric(sym1d: np.ndarray) -> np.ndarray:
n = int(np.sqrt(sym1d.size * 2))
assert (n * (n + 1)) // 2 == sym1d.size
R, C = np.triu_indices(n)
out = np.zeros((n, n), dtype=sym1d.dtype)
out[R, C] = sym1d
out[C, R] = sym1d
return out
������������cmaes-0.10.0/cmaes/_cmawm.py������������������������������������������������������������������������0000664�0000000�0000000�00000031425�14455660762�0015611�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import functools
import numpy as np
from typing import cast
from typing import Optional
from cmaes import CMA
from cmaes._cma import _is_valid_bounds
try:
from scipy import stats
chi2_ppf = functools.partial(stats.chi2.ppf, df=1)
norm_cdf = stats.norm.cdf
except ImportError:
from cmaes._stats import chi2_ppf # type: ignore
from cmaes._stats import norm_cdf
class CMAwM:
"""CMA-ES with Margin class with ask-and-tell interface.
The code is adapted from https://github.com/EvoConJP/CMA-ES_with_Margin.
Example:
.. code::
import numpy as np
from cmaes import CMAwM
def ellipsoid_onemax(x, n_zdim):
n = len(x)
n_rdim = n - n_zdim
ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
onemax = n_zdim - (0. < x[(n - n_zdim):]).sum()
return ellipsoid + 10 * onemax
binary_dim, continuous_dim = 10, 10
dim = binary_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([0, 1], (binary_dim, 1)),
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
]
)
steps = np.concatenate([np.ones(binary_dim), np.zeros(continuous_dim)])
optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_onemax(x_for_eval, binary_dim)
evals += 1
solutions.append((x_for_tell, value))
optimizer.tell(solutions)
if optimizer.should_stop():
break
Args:
mean:
Initial mean vector of multi-variate gaussian distributions.
sigma:
Initial standard deviation of covariance matrix.
bounds:
Lower and upper domain boundaries for each parameter.
steps:
Each value represents a step of discretization for each dimension.
Zero (or negative value) means a continuous space.
n_max_resampling:
A maximum number of resampling parameters (default: 100).
If all sampled parameters are infeasible, the last sampled one
will be clipped with lower and upper bounds.
seed:
A seed number (optional).
population_size:
A population size (optional).
cov:
A covariance matrix (optional).
margin:
A margin parameter (optional).
"""
# Paper: https://arxiv.org/abs/2205.13482
def __init__(
self,
mean: np.ndarray,
sigma: float,
bounds: np.ndarray,
steps: np.ndarray,
n_max_resampling: int = 100,
seed: Optional[int] = None,
population_size: Optional[int] = None,
cov: Optional[np.ndarray] = None,
margin: Optional[float] = None,
):
# initialize `CMA`
self._cma = CMA(
mean, sigma, bounds, n_max_resampling, seed, population_size, cov
)
n_dim = self._cma.dim
population_size = self._cma.population_size
self._n_max_resampling = n_max_resampling
# split discrete space and continuous space
assert len(bounds) == len(steps), "bounds and steps must be the same length"
assert not np.isnan(steps).any(), "steps should not include NaN"
self._discrete_idx = np.where(steps > 0)[0]
discrete_list = [
np.arange(bounds[i][0], bounds[i][1] + steps[i] / 2, steps[i])
for i in self._discrete_idx
]
max_discrete = max([len(discrete) for discrete in discrete_list], default=0)
discrete_space = np.full((len(self._discrete_idx), max_discrete), np.nan)
for i, discrete in enumerate(discrete_list):
discrete_space[i, : len(discrete)] = discrete
# continuous_space contains low and high of each parameter.
self._continuous_idx = np.where(steps <= 0)[0]
self._continuous_space = bounds[self._continuous_idx]
assert _is_valid_bounds(
self._continuous_space, mean[self._continuous_idx]
), "invalid bounds"
# discrete_space
self._n_zdim = len(discrete_space)
if self._n_zdim == 0:
return
self.margin = margin if margin is not None else 1 / (n_dim * population_size)
assert self.margin > 0, "margin must be non-zero positive value."
self.z_space = discrete_space
self.z_lim = (self.z_space[:, 1:] + self.z_space[:, :-1]) / 2
for i in range(self._n_zdim):
self.z_space[i][np.isnan(self.z_space[i])] = np.nanmax(self.z_space[i])
self.z_lim[i][np.isnan(self.z_lim[i])] = np.nanmax(self.z_lim[i])
self.z_lim_low = np.concatenate(
[self.z_lim.min(axis=1).reshape([self._n_zdim, 1]), self.z_lim], 1
)
self.z_lim_up = np.concatenate(
[self.z_lim, self.z_lim.max(axis=1).reshape([self._n_zdim, 1])], 1
)
m_z = self._cma._mean[self._discrete_idx].reshape(([self._n_zdim, 1]))
# m_z_lim_low ->| mean vector |<- m_z_lim_up
self.m_z_lim_low = (
self.z_lim_low
* np.where(np.sort(np.concatenate([self.z_lim, m_z], 1)) == m_z, 1, 0)
).sum(axis=1)
self.m_z_lim_up = (
self.z_lim_up
* np.where(np.sort(np.concatenate([self.z_lim, m_z], 1)) == m_z, 1, 0)
).sum(axis=1)
self._A = np.full(n_dim, 1.0)
@property
def dim(self) -> int:
"""A number of dimensions"""
return self._cma.dim
@property
def population_size(self) -> int:
"""A population size"""
return self._cma.population_size
@property
def generation(self) -> int:
"""Generation number which is monotonically incremented
when multi-variate gaussian distribution is updated."""
return self._cma.generation
@property
def _rng(self) -> np.random.RandomState:
return self._cma._rng
def reseed_rng(self, seed: int) -> None:
self._cma.reseed_rng(seed)
def ask(self) -> tuple[np.ndarray, np.ndarray]:
"""Sample a parameter and return (i) encoded x and (ii) raw x.
The encoded x is used for the evaluation.
The raw x is used for updating the distribution."""
for i in range(self._n_max_resampling):
x = self._cma._sample_solution()
if self._is_continuous_feasible(x[self._continuous_idx]):
x_encoded = x.copy()
if self._n_zdim > 0:
x_encoded[self._discrete_idx] = self._encode_discrete_params(
x[self._discrete_idx]
)
return x_encoded, x
x = self._cma._sample_solution()
x[self._continuous_idx] = self._repair_continuous_params(
x[self._continuous_idx]
)
x_encoded = x.copy()
if self._n_zdim > 0:
x_encoded[self._discrete_idx] = self._encode_discrete_params(
x[self._discrete_idx]
)
return x_encoded, x
def _is_continuous_feasible(self, continuous_param: np.ndarray) -> bool:
if self._continuous_space is None:
return True
return cast(
bool,
np.all(continuous_param >= self._continuous_space[:, 0])
and np.all(continuous_param <= self._continuous_space[:, 1]),
) # Cast bool_ to bool.
def _repair_continuous_params(self, continuous_param: np.ndarray) -> np.ndarray:
if self._continuous_space is None:
return continuous_param
# clip with lower and upper bound.
param = np.where(
continuous_param < self._continuous_space[:, 0],
self._continuous_space[:, 0],
continuous_param,
)
param = np.where(
param > self._continuous_space[:, 1], self._continuous_space[:, 1], param
)
return param
def _encode_discrete_params(self, discrete_param: np.ndarray) -> np.ndarray:
"""Encode the values into discrete domain."""
mean = self._cma._mean
x = (discrete_param - mean[self._discrete_idx]) * self._A[
self._discrete_idx
] + mean[self._discrete_idx]
x = x.reshape([self._n_zdim, 1])
x_enc = (
self.z_space
* np.where(np.sort(np.concatenate((self.z_lim, x), axis=1)) == x, 1, 0)
).sum(axis=1)
return x_enc.reshape(self._n_zdim)
def tell(self, solutions: list[tuple[np.ndarray, float]]) -> None:
"""Tell evaluation values"""
self._cma.tell(solutions)
mean = self._cma._mean
sigma = self._cma._sigma
C = self._cma._C
if self._n_zdim == 0:
return
# margin correction
updated_m_integer = mean[self._discrete_idx, np.newaxis]
self.z_lim_low = np.concatenate(
[self.z_lim.min(axis=1).reshape([self._n_zdim, 1]), self.z_lim], 1
)
self.z_lim_up = np.concatenate(
[self.z_lim, self.z_lim.max(axis=1).reshape([self._n_zdim, 1])], 1
)
self.m_z_lim_low = (
self.z_lim_low
* np.where(
np.sort(np.concatenate([self.z_lim, updated_m_integer], 1))
== updated_m_integer,
1,
0,
)
).sum(axis=1)
self.m_z_lim_up = (
self.z_lim_up
* np.where(
np.sort(np.concatenate([self.z_lim, updated_m_integer], 1))
== updated_m_integer,
1,
0,
)
).sum(axis=1)
# calculate probability low_cdf := Pr(X <= m_z_lim_low) and up_cdf := Pr(m_z_lim_up < X)
# sig_z_sq_Cdiag = self.model.sigma * self.model.A * np.sqrt(np.diag(self.model.C))
z_scale = (
sigma
* self._A[self._discrete_idx]
* np.sqrt(np.diag(C)[self._discrete_idx])
)
updated_m_integer = updated_m_integer.flatten()
low_cdf = norm_cdf(self.m_z_lim_low, loc=updated_m_integer, scale=z_scale)
up_cdf = 1.0 - norm_cdf(self.m_z_lim_up, loc=updated_m_integer, scale=z_scale)
mid_cdf = 1.0 - (low_cdf + up_cdf)
# edge case
edge_mask = np.maximum(low_cdf, up_cdf) > 0.5
# otherwise
side_mask = np.maximum(low_cdf, up_cdf) <= 0.5
if np.any(edge_mask):
# modify mask (modify or not)
modify_mask = np.minimum(low_cdf, up_cdf) < self.margin
# modify sign
modify_sign = np.sign(mean[self._discrete_idx] - self.m_z_lim_up)
# distance from m_z_lim_up
dist = (
sigma
* self._A[self._discrete_idx]
* np.sqrt(
chi2_ppf(q=1.0 - 2.0 * self.margin) * np.diag(C)[self._discrete_idx]
)
)
# modify mean vector
mean[self._discrete_idx] = mean[
self._discrete_idx
] + modify_mask * edge_mask * (
self.m_z_lim_up + modify_sign * dist - mean[self._discrete_idx]
)
# correct probability
low_cdf = np.maximum(low_cdf, self.margin / 2.0)
up_cdf = np.maximum(up_cdf, self.margin / 2.0)
modified_low_cdf = low_cdf + (1.0 - low_cdf - up_cdf - mid_cdf) * (
low_cdf - self.margin / 2
) / (low_cdf + mid_cdf + up_cdf - 3.0 * self.margin / 2)
modified_up_cdf = up_cdf + (1.0 - low_cdf - up_cdf - mid_cdf) * (
up_cdf - self.margin / 2
) / (low_cdf + mid_cdf + up_cdf - 3.0 * self.margin / 2)
modified_low_cdf = np.clip(modified_low_cdf, 1e-10, 0.5 - 1e-10)
modified_up_cdf = np.clip(modified_up_cdf, 1e-10, 0.5 - 1e-10)
# modify mean vector and A (with sigma and C fixed)
chi_low_sq = np.sqrt(chi2_ppf(q=1.0 - 2 * modified_low_cdf))
chi_up_sq = np.sqrt(chi2_ppf(q=1.0 - 2 * modified_up_cdf))
C_diag_sq = np.sqrt(np.diag(C))[self._discrete_idx]
# simultaneous equations
self._A[self._discrete_idx] = self._A[self._discrete_idx] + side_mask * (
(self.m_z_lim_up - self.m_z_lim_low)
/ ((chi_low_sq + chi_up_sq) * sigma * C_diag_sq)
- self._A[self._discrete_idx]
)
mean[self._discrete_idx] = mean[self._discrete_idx] + side_mask * (
(self.m_z_lim_low * chi_up_sq + self.m_z_lim_up * chi_low_sq)
/ (chi_low_sq + chi_up_sq)
- mean[self._discrete_idx]
)
def should_stop(self) -> bool:
return self._cma.should_stop()
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/_dxnesic.py����������������������������������������������������������������������0000664�0000000�0000000�00000034425�14455660762�0016145�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import math
import sys
import numpy as np
from typing import cast
from typing import Optional
_EPS = 1e-8
_MEAN_MAX = 1e32
_SIGMA_MAX = 1e32
class DXNESIC:
"""DX-NES-IC stochastic optimizer class with ask-and-tell interface.
Example:
.. code::
import numpy as np
from cmaes import DXNESIC
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
optimizer = DXNESIC(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
# Tell evaluation values.
optimizer.tell(solutions)
Args:
mean:
Initial mean vector of multi-variate gaussian distributions.
sigma:
Initial standard deviation of covariance matrix.
bounds:
Lower and upper domain boundaries for each parameter (optional).
n_max_resampling:
A maximum number of resampling parameters (default: 100).
If all sampled parameters are infeasible, the last sampled one
will be clipped with lower and upper bounds.
seed:
A seed number (optional).
population_size:
A population size (optional).
cov:
A covariance matrix (optional).
"""
# Paper: https://ieeexplore.ieee.org/abstract/document/9504865
def __init__(
self,
mean: np.ndarray,
sigma: float,
bounds: Optional[np.ndarray] = None,
n_max_resampling: int = 100,
seed: Optional[int] = None,
population_size: Optional[int] = None,
):
assert sigma > 0, "sigma must be non-zero positive value"
assert np.all(
np.abs(mean) < _MEAN_MAX
), f"Abs of all elements of mean vector must be less than {_MEAN_MAX}"
n_dim = len(mean)
assert n_dim > 1, "The dimension of mean must be larger than 1"
if population_size is None:
population_size = 4 + math.floor(3 * math.log(n_dim))
assert population_size > 0, "popsize must be non-zero positive value."
w_rank_hat = np.log(population_size / 2 + 1) - np.log(
np.arange(1, population_size + 1)
)
w_rank_hat[np.where(w_rank_hat < 0)] = 0
w_rank = w_rank_hat / sum(w_rank_hat) - (1.0 / population_size)
mu_eff = 1 / sum((w_rank + (1.0 / population_size)) ** 2)
# learning rate for the cumulation for the step-size control
c_sigma = (mu_eff + 2) / (n_dim + mu_eff + 5)
assert (
c_sigma < 1
), "invalid learning rate for cumulation for the step-size control"
# distance weight parameter
h_inv = _get_h_inv(n_dim)
self._n_dim = n_dim
self._popsize = population_size
self._mu_eff = mu_eff
self._h_inv = h_inv
self._c_sigma = c_sigma
# E||N(0, I)||
self._chi_n = math.sqrt(self._n_dim) * (
1.0 - (1.0 / (4.0 * self._n_dim)) + 1.0 / (21.0 * (self._n_dim**2))
)
# weights
self._w_rank = w_rank
self._w_rank_hat = w_rank_hat
# for antithetic sampling
self._zsym: Optional[np.ndarray] = None
# learning rate
self._eta_mean = 1.0
self._eta_move_sigma = 1.0
self._c_gamma = 1.0 / (3.0 * (n_dim - 1.0))
self._d_gamma = min(1.0, n_dim / population_size)
self._gamma = 1.0
# evolution path
self._p_sigma = np.zeros(n_dim)
# distribution parameter
self._mean = mean.copy()
self._sigma = sigma
self._B = np.eye(n_dim)
# bounds contains low and high of each parameter.
assert bounds is None or _is_valid_bounds(bounds, mean), "invalid bounds"
self._bounds = bounds
self._n_max_resampling = n_max_resampling
self._g = 0
self._rng = np.random.RandomState(seed)
# Termination criteria
self._tolx = 1e-12 * sigma
self._tolxup = 1e4
self._tolfun = 1e-12
self._tolconditioncov = 1e14
self._funhist_term = 10 + math.ceil(30 * n_dim / population_size)
self._funhist_values = np.empty(self._funhist_term * 2)
@property
def dim(self) -> int:
"""A number of dimensions"""
return self._n_dim
@property
def population_size(self) -> int:
"""A population size"""
return self._popsize
@property
def generation(self) -> int:
"""Generation number which is monotonically incremented
when multi-variate gaussian distribution is updated."""
return self._g
def _alpha_dist(self, num_feasible: int) -> float:
return (
self._h_inv
* min(1.0, math.sqrt(float(self._popsize) / self._n_dim))
* math.sqrt(float(num_feasible) / self._popsize)
)
def _w_dist_hat(self, z: np.ndarray, num_feasible: int) -> float:
return math.exp(self._alpha_dist(num_feasible) * np.linalg.norm(z))
def _eta_stag_sigma(self, num_feasible: int) -> float:
return math.tanh(
(0.024 * num_feasible + 0.7 * self._n_dim + 20.0) / (self._n_dim + 12.0)
)
def _eta_conv_sigma(self, num_feasible: int) -> float:
return 2.0 * math.tanh(
(0.025 * num_feasible + 0.75 * self._n_dim + 10.0) / (self._n_dim + 4.0)
)
def _eta_move_B(self, num_feasible: int) -> float:
return (
180
* self._n_dim
* math.tanh(0.02 * num_feasible)
/ (47 * (self._n_dim**2) + 6400)
)
def _eta_stag_B(self, num_feasible: int) -> float:
return (
168
* self._n_dim
* math.tanh(0.02 * num_feasible)
/ (47 * (self._n_dim**2) + 6400)
)
def _eta_conv_B(self, num_feasible: int) -> float:
return (
12
* self._n_dim
* math.tanh(0.02 * num_feasible)
/ (47 * (self._n_dim**2) + 6400)
)
def reseed_rng(self, seed: int) -> None:
self._rng.seed(seed)
def set_bounds(self, bounds: Optional[np.ndarray]) -> None:
"""Update boundary constraints"""
assert bounds is None or _is_valid_bounds(bounds, self._mean), "invalid bounds"
self._bounds = bounds
def ask(self) -> np.ndarray:
"""Sample a parameter"""
for i in range(self._n_max_resampling):
x = self._sample_solution()
if self._is_feasible(x):
return x
x = self._sample_solution()
x = self._repair_infeasible_params(x)
return x
def _sample_solution(self) -> np.ndarray:
# antithetic sampling
if self._zsym is None:
z = self._rng.randn(self._n_dim) # ~ N(0, I)
self._zsym = z
else:
z = -self._zsym
self._zsym = None
x = self._mean + self._sigma * self._B.dot(z) # ~ N(m, σ^2 B B^T)
return x
def _is_feasible(self, param: np.ndarray) -> bool:
if self._bounds is None:
return True
return cast(
bool,
np.all(param >= self._bounds[:, 0]) and np.all(param <= self._bounds[:, 1]),
) # Cast bool_ to bool.
def _repair_infeasible_params(self, param: np.ndarray) -> np.ndarray:
if self._bounds is None:
return param
# clip with lower and upper bound.
param = np.where(param < self._bounds[:, 0], self._bounds[:, 0], param)
param = np.where(param > self._bounds[:, 1], self._bounds[:, 1], param)
return param
def tell(self, solutions: list[tuple[np.ndarray, float]]) -> None:
"""Tell evaluation values"""
assert len(solutions) == self._popsize, "Must tell popsize-length solutions."
for s in solutions:
assert np.all(
np.abs(s[0]) < _MEAN_MAX
), f"Abs of all param values must be less than {_MEAN_MAX} to avoid overflow errors"
# counting # feasible solutions
lamb_feas = len([s[1] for s in solutions if s[1] < sys.maxsize])
self._g += 1
solutions.sort(key=lambda s: s[1])
# Stores 'best' and 'worst' values of the
# last 'self._funhist_term' generations.
funhist_idx = 2 * (self.generation % self._funhist_term)
self._funhist_values[funhist_idx] = solutions[0][1]
self._funhist_values[funhist_idx + 1] = solutions[-1][1]
z_k = np.array(
[
np.linalg.inv(self._sigma * self._B).dot(s[0] - self._mean)
for s in solutions
]
)
# Evolution path
z_w = np.sum(z_k.T * self._w_rank, axis=1)
self._p_sigma = (1 - self._c_sigma) * self._p_sigma + math.sqrt(
self._c_sigma * (2 - self._c_sigma) * self._mu_eff
) * z_w
norm_p_sigma = np.linalg.norm(self._p_sigma)
# switching learning rate depending on search situation
movement_phase = norm_p_sigma >= self._chi_n
# distance weight
w_dist_tmp = np.array(
[
self._w_rank_hat[i] * self._w_dist_hat(z_k[i, :], lamb_feas)
for i in range(self.population_size)
]
)
w_dist = w_dist_tmp / sum(w_dist_tmp) - 1.0 / self.population_size
# switching weights and learning rate
w = w_dist if movement_phase else self._w_rank
eta_sigma = (
self._eta_move_sigma
if norm_p_sigma >= self._chi_n
else self._eta_stag_sigma(lamb_feas)
if norm_p_sigma >= 0.1 * self._chi_n
else self._eta_conv_sigma(lamb_feas)
)
eta_B = (
self._eta_move_B(lamb_feas)
if norm_p_sigma >= self._chi_n
else self._eta_stag_B(lamb_feas)
if norm_p_sigma >= 0.1 * self._chi_n
else self._eta_conv_B(lamb_feas)
)
# natural gradient estimation in local coordinate
G_delta = np.sum(
[w[i] * z_k[i, :] for i in range(self.population_size)], axis=0
)
G_M = np.sum(
[
w[i] * (np.outer(z_k[i, :], z_k[i, :]) - np.eye(self._n_dim))
for i in range(self.population_size)
],
axis=0,
)
G_sigma = G_M.trace() / self._n_dim
G_B = G_M - G_sigma * np.eye(self._n_dim)
# parameter update
bBBT = self._B @ self._B.T
self._mean += self._eta_mean * self._sigma * np.dot(self._B, G_delta)
self._sigma *= math.exp((eta_sigma / 2.0) * G_sigma)
# self._B = self._B.dot(expm((eta_B / 2.0) * G_B))
self._B = self._B.dot(_expm((eta_B / 2.0) * G_B))
aBBT = self._B @ self._B.T
# emphasizing expansion
e, v = np.linalg.eigh(bBBT)
tau_vec = [
(v[:, i].reshape(self._n_dim, 1).T @ aBBT @ v[:, i].reshape(self._n_dim, 1))
/ (
v[:, i].reshape(self._n_dim, 1).T
@ bBBT
@ v[:, i].reshape(self._n_dim, 1)
)
- 1
for i in range(self._n_dim)
]
flg_tau = [1.0 if tau_vec[i] > 0 else 0.0 for i in range(self._n_dim)]
tau = max(tau_vec)
gamma = max(
(1.0 - self._c_gamma) * self._gamma
+ self._c_gamma * math.sqrt(1.0 + self._d_gamma * tau),
1.0,
)
if movement_phase:
Q = (gamma - 1.0) * np.sum(
[flg_tau[i] * np.outer(v[:, i], v[:, i]) for i in range(self._n_dim)],
axis=0,
) + np.eye(self._n_dim)
stepQ = math.pow(np.linalg.det(Q), 1.0 / self._n_dim)
self._sigma *= stepQ
self._B = Q @ self._B / stepQ
def should_stop(self) -> bool:
A = self._B.dot(self._B.T)
A = (A + A.T) / 2
E2, V = np.linalg.eigh(A)
E = np.sqrt(np.where(E2 < 0, _EPS, E2))
diagA = np.diag(A)
# Stop if the range of function values of the recent generation is below tolfun.
if (
self.generation > self._funhist_term
and np.max(self._funhist_values) - np.min(self._funhist_values)
< self._tolfun
):
return True
# Stop if detecting divergent behavior.
if self._sigma * np.max(E) > self._tolxup:
return True
# No effect coordinates: stop if adding 0.2-standard deviations
# in any single coordinate does not change m.
if np.any(self._mean == self._mean + (0.2 * self._sigma * np.sqrt(diagA))):
return True
# No effect axis: stop if adding 0.1-standard deviation vector in
# any principal axis direction of C does not change m. "pycma" check
# axis one by one at each generation.
i = self.generation % self.dim
if np.all(self._mean == self._mean + (0.1 * self._sigma * E[i] * V[:, i])):
return True
# Stop if the condition number of the covariance matrix exceeds 1e14.
condition_cov = np.max(E) / np.min(E)
if condition_cov > self._tolconditioncov:
return True
return False
def _is_valid_bounds(bounds: Optional[np.ndarray], mean: np.ndarray) -> bool:
if bounds is None:
return True
if (mean.size, 2) != bounds.shape:
return False
if not np.all(bounds[:, 0] <= mean):
return False
if not np.all(mean <= bounds[:, 1]):
return False
return True
def _get_h_inv(dim: int) -> float:
def f(a: float) -> float:
return ((1.0 + a * a) * math.exp(a * a / 2.0) / 0.24) - 10.0 - dim
def f_prime(a: float) -> float:
return (1.0 / 0.24) * a * math.exp(a * a / 2.0) * (3.0 + a * a)
h_inv = 6.0
while abs(f(h_inv)) > 1e-10:
last = h_inv
h_inv = h_inv - 0.5 * (f(h_inv) / f_prime(h_inv))
if abs(h_inv - last) < 1e-16:
# Exit early since no further improvements are happening
break
return h_inv
def _expm(mat: np.ndarray) -> np.ndarray:
D, U = np.linalg.eigh(mat)
expD = np.exp(D)
return U @ np.diag(expD) @ U.T
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/_sepcma.py�����������������������������������������������������������������������0000664�0000000�0000000�00000027360�14455660762�0015760�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import math
import numpy as np
from typing import Any
from typing import cast
from typing import Optional
_EPS = 1e-8
_MEAN_MAX = 1e32
_SIGMA_MAX = 1e32
class SepCMA:
"""Separable CMA-ES stochastic optimizer class with ask-and-tell interface.
Example:
.. code::
import numpy as np
from cmaes import SepCMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
optimizer = SepCMA(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
# Tell evaluation values.
optimizer.tell(solutions)
Args:
mean:
Initial mean vector of multi-variate gaussian distributions.
sigma:
Initial standard deviation of covariance matrix.
bounds:
Lower and upper domain boundaries for each parameter (optional).
n_max_resampling:
A maximum number of resampling parameters (default: 100).
If all sampled parameters are infeasible, the last sampled one
will be clipped with lower and upper bounds.
seed:
A seed number (optional).
population_size:
A population size (optional).
"""
def __init__(
self,
mean: np.ndarray,
sigma: float,
bounds: Optional[np.ndarray] = None,
n_max_resampling: int = 100,
seed: Optional[int] = None,
population_size: Optional[int] = None,
):
assert sigma > 0, "sigma must be non-zero positive value"
assert np.all(
np.abs(mean) < _MEAN_MAX
), f"Abs of all elements of mean vector must be less than {_MEAN_MAX}"
n_dim = len(mean)
assert n_dim > 1, "The dimension of mean must be larger than 1"
if population_size is None:
population_size = 4 + math.floor(3 * math.log(n_dim)) # (eq. 48)
assert population_size > 0, "popsize must be non-zero positive value."
mu = population_size // 2
# (eq.49)
weights_prime = np.array(
[math.log(mu + 1) - math.log(i + 1) for i in range(mu)]
)
weights = weights_prime / sum(weights_prime)
mu_eff = 1 / sum(weights**2)
# learning rate for the rank-one update
alpha_cov = 2
c1 = alpha_cov / ((n_dim + 1.3) ** 2 + mu_eff)
# learning rate for the rank-μ update
cmu_full = 2 / mu_eff / ((n_dim + np.sqrt(2)) ** 2) + (1 - 1 / mu_eff) * min(
1, (2 * mu_eff - 1) / ((n_dim + 2) ** 2 + mu_eff)
)
cmu = (n_dim + 2) / 3 * cmu_full
cm = 1 # (eq. 54)
# learning rate for the cumulation for the step-size control
c_sigma = (mu_eff + 2) / (n_dim + mu_eff + 3)
d_sigma = 1 + 2 * max(0, math.sqrt((mu_eff - 1) / (n_dim + 1)) - 1) + c_sigma
assert (
c_sigma < 1
), "invalid learning rate for cumulation for the step-size control"
# learning rate for cumulation for the rank-one update
cc = 4 / (n_dim + 4)
assert cc <= 1, "invalid learning rate for cumulation for the rank-one update"
self._n_dim = n_dim
self._popsize = population_size
self._mu = mu
self._mu_eff = mu_eff
self._cc = cc
self._c1 = c1
self._cmu = cmu
self._c_sigma = c_sigma
self._d_sigma = d_sigma
self._cm = cm
# E||N(0, I)|| (p.28)
self._chi_n = math.sqrt(self._n_dim) * (
1.0 - (1.0 / (4.0 * self._n_dim)) + 1.0 / (21.0 * (self._n_dim**2))
)
self._weights = weights
# evolution path
self._p_sigma = np.zeros(n_dim)
self._pc = np.zeros(n_dim)
self._mean = mean
self._sigma = sigma
self._D: Optional[np.ndarray] = None
self._C: np.ndarray = np.ones(n_dim)
# bounds contains low and high of each parameter.
assert bounds is None or _is_valid_bounds(bounds, mean), "invalid bounds"
self._bounds = bounds
self._n_max_resampling = n_max_resampling
self._g = 0
self._rng = np.random.RandomState(seed)
# Termination criteria
self._tolx = 1e-12 * sigma
self._tolxup = 1e4
self._tolfun = 1e-12
self._tolconditioncov = 1e14
self._funhist_term = 10 + math.ceil(30 * n_dim / population_size)
self._funhist_values = np.empty(self._funhist_term * 2)
@property
def dim(self) -> int:
"""A number of dimensions"""
return self._n_dim
@property
def population_size(self) -> int:
"""A population size"""
return self._popsize
@property
def generation(self) -> int:
"""Generation number which is monotonically incremented
when multi-variate gaussian distribution is updated."""
return self._g
def reseed_rng(self, seed: int) -> None:
self._rng.seed(seed)
def __getstate__(self) -> dict[str, Any]:
attrs = {}
for name in self.__dict__:
# Remove _rng in pickle serialized object.
if name == "_rng":
continue
attrs[name] = getattr(self, name)
return attrs
def __setstate__(self, state: dict[str, Any]) -> None:
self.__dict__.update(state)
# Set _rng for unpickled object.
setattr(self, "_rng", np.random.RandomState())
def set_bounds(self, bounds: Optional[np.ndarray]) -> None:
"""Update boundary constraints"""
assert bounds is None or _is_valid_bounds(bounds, self._mean), "invalid bounds"
self._bounds = bounds
def ask(self) -> np.ndarray:
"""Sample a parameter"""
for i in range(self._n_max_resampling):
x = self._sample_solution()
if self._is_feasible(x):
return x
x = self._sample_solution()
x = self._repair_infeasible_params(x)
return x
def _eigen_decomposition(self) -> np.ndarray:
if self._D is not None:
return self._D
self._D = np.sqrt(np.where(self._C < 0, _EPS, self._C))
return self._D
def _sample_solution(self) -> np.ndarray:
D = self._eigen_decomposition()
z = self._rng.randn(self._n_dim) # ~ N(0, I)
y = D * z # ~ N(0, C)
x = self._mean + self._sigma * y # ~ N(m, σ^2 C)
return x
def _is_feasible(self, param: np.ndarray) -> bool:
if self._bounds is None:
return True
return cast(
bool,
np.all(param >= self._bounds[:, 0]) and np.all(param <= self._bounds[:, 1]),
) # Cast bool_ to bool
def _repair_infeasible_params(self, param: np.ndarray) -> np.ndarray:
if self._bounds is None:
return param
# clip with lower and upper bound.
param = np.where(param < self._bounds[:, 0], self._bounds[:, 0], param)
param = np.where(param > self._bounds[:, 1], self._bounds[:, 1], param)
return param
def tell(self, solutions: list[tuple[np.ndarray, float]]) -> None:
"""Tell evaluation values"""
assert len(solutions) == self._popsize, "Must tell popsize-length solutions."
for s in solutions:
assert np.all(
np.abs(s[0]) < _MEAN_MAX
), f"Abs of all param values must be less than {_MEAN_MAX} to avoid overflow errors"
self._g += 1
solutions.sort(key=lambda s: s[1])
# Stores 'best' and 'worst' values of the
# last 'self._funhist_term' generations.
funhist_idx = 2 * (self.generation % self._funhist_term)
self._funhist_values[funhist_idx] = solutions[0][1]
self._funhist_values[funhist_idx + 1] = solutions[-1][1]
# Sample new population of search_points, for k=1, ..., popsize
D = self._eigen_decomposition()
self._D = None
x_k = np.array([s[0] for s in solutions]) # ~ N(m, σ^2 C)
y_k = (x_k - self._mean) / self._sigma # ~ N(0, C)
# Selection and recombination
y_w = np.sum(y_k[: self._mu].T * self._weights[: self._mu], axis=1)
self._mean += self._cm * self._sigma * y_w
# Step-size control
self._p_sigma = (1 - self._c_sigma) * self._p_sigma + math.sqrt(
self._c_sigma * (2 - self._c_sigma) * self._mu_eff
) * (y_w / D)
norm_p_sigma = np.linalg.norm(self._p_sigma)
self._sigma *= np.exp(
(self._c_sigma / self._d_sigma) * (norm_p_sigma / self._chi_n - 1)
)
self._sigma = min(self._sigma, _SIGMA_MAX)
# Covariance matrix adaption
h_sigma_cond_left = norm_p_sigma / math.sqrt(
1 - (1 - self._c_sigma) ** (2 * (self._g + 1))
)
h_sigma_cond_right = (1.4 + 2 / (self._n_dim + 1)) * self._chi_n
h_sigma = 1.0 if h_sigma_cond_left < h_sigma_cond_right else 0.0 # (p.28)
# (eq.45)
self._pc = (1 - self._cc) * self._pc + h_sigma * math.sqrt(
self._cc * (2 - self._cc) * self._mu_eff
) * y_w
delta_h_sigma = (1 - h_sigma) * self._cc * (2 - self._cc) # (p.28)
assert delta_h_sigma <= 1
# (eq.47)
rank_one = self._pc**2
rank_mu = np.sum(
np.array([w * (y**2) for w, y in zip(self._weights, y_k)]), axis=0
)
self._C = (
(
1
+ self._c1 * delta_h_sigma
- self._c1
- self._cmu * np.sum(self._weights)
)
* self._C
+ self._c1 * rank_one
+ self._cmu * rank_mu
)
def should_stop(self) -> bool:
D = self._eigen_decomposition()
# Stop if the range of function values of the recent generation is below tolfun.
if (
self.generation > self._funhist_term
and np.max(self._funhist_values) - np.min(self._funhist_values)
< self._tolfun
):
return True
# Stop if the std of the normal distribution is smaller than tolx
# in all coordinates and pc is smaller than tolx in all components.
if np.all(self._sigma * self._C < self._tolx) and np.all(
self._sigma * self._pc < self._tolx
):
return True
# Stop if detecting divergent behavior.
if self._sigma * np.max(D) > self._tolxup:
return True
# No effect coordinates: stop if adding 0.2-standard deviations
# in any single coordinate does not change m.
if np.any(self._mean == self._mean + (0.2 * self._sigma * np.sqrt(self._C))):
return True
# No effect axis: stop if adding 0.1-standard deviation vector in
# any principal axis direction of C does not change m. "pycma" check
# axis one by one at each generation.
i = self.generation % self.dim
if np.all(
self._mean == self._mean + (0.1 * self._sigma * D[i] * np.ones(self._n_dim))
):
return True
# Stop if the condition number of the covariance matrix exceeds 1e14.
condition_cov = np.max(D) / np.min(D)
if condition_cov > self._tolconditioncov:
return True
return False
def _is_valid_bounds(bounds: Optional[np.ndarray], mean: np.ndarray) -> bool:
if bounds is None:
return True
if (mean.size, 2) != bounds.shape:
return False
if not np.all(bounds[:, 0] <= mean):
return False
if not np.all(mean <= bounds[:, 1]):
return False
return True
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/_stats.py������������������������������������������������������������������������0000664�0000000�0000000�00000001751�14455660762�0015642�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import math
import numpy as np
@np.vectorize
def norm_cdf(x: float, loc: float = 0.0, scale: float = 1.0) -> float:
x = (x - loc) / scale
x = x / 2**0.5
z = abs(x)
if z < 1 / 2**0.5:
y = 0.5 + 0.5 * math.erf(x)
else:
y = 0.5 * math.erfc(z)
if x > 0:
y = 1.0 - y
return y
@np.vectorize
def chi2_ppf(q: float) -> float:
"""
only deal with the special case df=1, loc=0, scale=1
solve chi2.cdf(x; df=1) = erf(sqrt(x/2)) = q with bisection method
"""
if q == 0:
return 0.0
if q == 1:
return math.inf
a, b = 0.0, 100.0
if q < 0.9:
for _ in range(100):
m = (a + b) / 2
if math.erf(math.sqrt(m / 2)) < q:
a = m
else:
b = m
else:
for _ in range(100):
m = (a + b) / 2
if math.erfc(math.sqrt(m / 2)) > 1.0 - q:
a = m
else:
b = m
return m
�����������������������cmaes-0.10.0/cmaes/_warm_start.py�������������������������������������������������������������������0000664�0000000�0000000�00000004663�14455660762�0016674�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import math
import numpy as np
def get_warm_start_mgd(
source_solutions: list[tuple[np.ndarray, float]],
gamma: float = 0.1,
alpha: float = 0.1,
) -> tuple[np.ndarray, float, np.ndarray]:
"""Estimates a promising distribution of the source task, then
returns a multivariate gaussian distribution (the mean vector
and the covariance matrix) used for initialization of the CMA-ES.
Args:
source_solutions:
List of solutions (parameter, value) on a source task.
gamma:
top-(gamma x 100)% solutions are selected from a set of solutions
on a source task. (default: 0.1).
alpha:
prior parameter for the initial covariance matrix (default: 0.1).
Returns:
The tuple of mean vector, sigma, and covariance matrix.
"""
# Paper: https://arxiv.org/abs/2012.06932
assert 0 < gamma <= 1, "gamma should be in (0, 1]"
if len(source_solutions) == 0:
raise ValueError("solutions should contain one or more items.")
# Select top-(gamma x 100)% solutions
source_solutions = sorted(source_solutions, key=lambda t: t[1])
gamma_n = math.floor(len(source_solutions) * gamma)
assert gamma_n >= 1, "One or more solutions must be selected from a source task"
dim = len(source_solutions[0][0])
top_gamma_solutions = np.empty(
shape=(
gamma_n,
dim,
),
dtype=float,
)
for i in range(gamma_n):
top_gamma_solutions[i] = source_solutions[i][0]
# Estimation of a Promising Distribution of a Source Task.
first_term = alpha**2 * np.eye(dim)
cov_term = np.zeros(shape=(dim, dim), dtype=float)
for i in range(gamma_n):
cov_term += np.dot(
top_gamma_solutions[i, :].reshape(dim, 1),
top_gamma_solutions[i, :].reshape(dim, 1).T,
)
second_term = cov_term / gamma_n
mean_term = np.zeros(
shape=(
dim,
1,
),
dtype=float,
)
for i in range(gamma_n):
mean_term += top_gamma_solutions[i, :].reshape(dim, 1)
mean_term /= gamma_n
third_term = np.dot(mean_term, mean_term.T)
mu = mean_term
mean = mu[:, 0]
Sigma = first_term + second_term - third_term
det_sigma = np.linalg.det(Sigma)
sigma = math.pow(det_sigma, 1.0 / 2.0 / dim)
cov = Sigma / math.pow(det_sigma, 1.0 / dim)
return mean, sigma, cov
�����������������������������������������������������������������������������cmaes-0.10.0/cmaes/_xnes.py�������������������������������������������������������������������������0000664�0000000�0000000�00000021510�14455660762�0015454�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from __future__ import annotations
import math
import numpy as np
from typing import cast
from typing import Optional
_EPS = 1e-8
_MEAN_MAX = 1e32
_SIGMA_MAX = 1e32
class XNES:
"""xNES stochastic optimizer class with ask-and-tell interface.
Example:
.. code::
import numpy as np
from cmaes import XNES
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
optimizer = XNES(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
# Tell evaluation values.
optimizer.tell(solutions)
Args:
mean:
Initial mean vector of multi-variate gaussian distributions.
sigma:
Initial standard deviation of covariance matrix.
bounds:
Lower and upper domain boundaries for each parameter (optional).
n_max_resampling:
A maximum number of resampling parameters (default: 100).
If all sampled parameters are infeasible, the last sampled one
will be clipped with lower and upper bounds.
seed:
A seed number (optional).
population_size:
A population size (optional).
"""
# Paper: https://dl.acm.org/doi/10.1145/1830483.1830557
def __init__(
self,
mean: np.ndarray,
sigma: float,
bounds: Optional[np.ndarray] = None,
n_max_resampling: int = 100,
seed: Optional[int] = None,
population_size: Optional[int] = None,
):
assert sigma > 0, "sigma must be non-zero positive value"
assert np.all(
np.abs(mean) < _MEAN_MAX
), f"Abs of all elements of mean vector must be less than {_MEAN_MAX}"
n_dim = len(mean)
assert n_dim > 1, "The dimension of mean must be larger than 1"
if population_size is None:
population_size = 4 + math.floor(3 * math.log(n_dim))
assert population_size > 0, "popsize must be non-zero positive value."
w_hat = np.log(population_size / 2 + 1) - np.log(
np.arange(1, population_size + 1)
)
w_hat[np.where(w_hat < 0)] = 0
weights = w_hat / sum(w_hat) - (1.0 / population_size)
self._n_dim = n_dim
self._popsize = population_size
# weights
self._weights = weights
# learning rate
self._eta_mean = 1.0
self._eta_sigma = (3 / 5) * (3 + math.log(n_dim)) / (n_dim * math.sqrt(n_dim))
self._eta_B = self._eta_sigma
# distribution parameter
self._mean = mean.copy()
self._sigma = sigma
self._B = np.eye(n_dim)
# bounds contains low and high of each parameter.
assert bounds is None or _is_valid_bounds(bounds, mean), "invalid bounds"
self._bounds = bounds
self._n_max_resampling = n_max_resampling
self._g = 0
self._rng = np.random.RandomState(seed)
# Termination criteria
self._tolx = 1e-12 * sigma
self._tolxup = 1e4
self._tolfun = 1e-12
self._tolconditioncov = 1e14
self._funhist_term = 10 + math.ceil(30 * n_dim / population_size)
self._funhist_values = np.empty(self._funhist_term * 2)
@property
def dim(self) -> int:
"""A number of dimensions"""
return self._n_dim
@property
def population_size(self) -> int:
"""A population size"""
return self._popsize
@property
def generation(self) -> int:
"""Generation number which is monotonically incremented
when multi-variate gaussian distribution is updated."""
return self._g
def reseed_rng(self, seed: int) -> None:
self._rng.seed(seed)
def set_bounds(self, bounds: Optional[np.ndarray]) -> None:
"""Update boundary constraints"""
assert bounds is None or _is_valid_bounds(bounds, self._mean), "invalid bounds"
self._bounds = bounds
def ask(self) -> np.ndarray:
"""Sample a parameter"""
for i in range(self._n_max_resampling):
x = self._sample_solution()
if self._is_feasible(x):
return x
x = self._sample_solution()
x = self._repair_infeasible_params(x)
return x
def _sample_solution(self) -> np.ndarray:
z = self._rng.randn(self._n_dim) # ~ N(0, I)
x = self._mean + self._sigma * self._B.dot(z) # ~ N(m, σ^2 B B^T)
return x
def _is_feasible(self, param: np.ndarray) -> bool:
if self._bounds is None:
return True
return cast(
bool,
np.all(param >= self._bounds[:, 0]) and np.all(param <= self._bounds[:, 1]),
) # Cast bool_ to bool.
def _repair_infeasible_params(self, param: np.ndarray) -> np.ndarray:
if self._bounds is None:
return param
# clip with lower and upper bound.
param = np.where(param < self._bounds[:, 0], self._bounds[:, 0], param)
param = np.where(param > self._bounds[:, 1], self._bounds[:, 1], param)
return param
def tell(self, solutions: list[tuple[np.ndarray, float]]) -> None:
"""Tell evaluation values"""
assert len(solutions) == self._popsize, "Must tell popsize-length solutions."
for s in solutions:
assert np.all(
np.abs(s[0]) < _MEAN_MAX
), f"Abs of all param values must be less than {_MEAN_MAX} to avoid overflow errors"
self._g += 1
solutions.sort(key=lambda s: s[1])
# Stores 'best' and 'worst' values of the
# last 'self._funhist_term' generations.
funhist_idx = 2 * (self.generation % self._funhist_term)
self._funhist_values[funhist_idx] = solutions[0][1]
self._funhist_values[funhist_idx + 1] = solutions[-1][1]
z_k = np.array(
[
np.linalg.inv(self._sigma * self._B).dot(s[0] - self._mean)
for s in solutions
]
)
# natural gradient estimation in local coordinate
G_delta = np.sum(
[self._weights[i] * z_k[i, :] for i in range(self.population_size)], axis=0
)
G_M = np.sum(
[
self._weights[i]
* (np.outer(z_k[i, :], z_k[i, :]) - np.eye(self._n_dim))
for i in range(self.population_size)
],
axis=0,
)
G_sigma = G_M.trace() / self._n_dim
G_B = G_M - G_sigma * np.eye(self._n_dim)
# parameter update
self._mean += self._eta_mean * self._sigma * np.dot(self._B, G_delta)
self._sigma *= math.exp((self._eta_sigma / 2.0) * G_sigma)
self._B = self._B.dot(_expm((self._eta_B / 2.0) * G_B))
def should_stop(self) -> bool:
A = self._B.dot(self._B.T)
A = (A + A.T) / 2
E2, V = np.linalg.eigh(A)
E = np.sqrt(np.where(E2 < 0, _EPS, E2))
diagA = np.diag(A)
# Stop if the range of function values of the recent generation is below tolfun.
if (
self.generation > self._funhist_term
and np.max(self._funhist_values) - np.min(self._funhist_values)
< self._tolfun
):
return True
# Stop if detecting divergent behavior.
if self._sigma * np.max(E) > self._tolxup:
return True
# No effect coordinates: stop if adding 0.2-standard deviations
# in any single coordinate does not change m.
if np.any(self._mean == self._mean + (0.2 * self._sigma * np.sqrt(diagA))):
return True
# No effect axis: stop if adding 0.1-standard deviation vector in
# any principal axis direction of C does not change m. "pycma" check
# axis one by one at each generation.
i = self.generation % self.dim
if np.all(self._mean == self._mean + (0.1 * self._sigma * E[i] * V[:, i])):
return True
# Stop if the condition number of the covariance matrix exceeds 1e14.
condition_cov = np.max(E) / np.min(E)
if condition_cov > self._tolconditioncov:
return True
return False
def _is_valid_bounds(bounds: Optional[np.ndarray], mean: np.ndarray) -> bool:
if bounds is None:
return True
if (mean.size, 2) != bounds.shape:
return False
if not np.all(bounds[:, 0] <= mean):
return False
if not np.all(mean <= bounds[:, 1]):
return False
return True
def _expm(mat: np.ndarray) -> np.ndarray:
D, U = np.linalg.eigh(mat)
expD = np.exp(D)
return U @ np.diag(expD) @ U.T
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/cmaes/cma.py���������������������������������������������������������������������������0000664�0000000�0000000�00000000323�14455660762�0015077�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import warnings
from ._cma import CMA
__all__ = ["CMA"]
warnings.warn(
"This module is deprecated. Please import CMA class from the "
"package root (ex: from cmaes import CMA).",
FutureWarning,
)
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0014515�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/bipop_cmaes.py����������������������������������������������������������������0000664�0000000�0000000�00000004631�14455660762�0017354�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1**2 + x2**2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e
+ 20
)
def main():
seed = 0
rng = np.random.RandomState(0)
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (rng.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
n_restarts = 0 # A small restart doesn't count in the n_restarts
small_n_eval, large_n_eval = 0, 0
popsize0 = optimizer.population_size
inc_popsize = 2
# Initial run is with "normal" population size; it is
# the large population before first doubling, but its
# budget accounting is the same as in case of small
# population.
poptype = "small"
while n_restarts <= 5:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
# print("{:10.5f} {:6.2f} {:6.2f}".format(value, x[0], x[1]))
optimizer.tell(solutions)
if optimizer.should_stop():
seed += 1
n_eval = optimizer.population_size * optimizer.generation
if poptype == "small":
small_n_eval += n_eval
else: # poptype == "large"
large_n_eval += n_eval
if small_n_eval < large_n_eval:
poptype = "small"
popsize_multiplier = inc_popsize**n_restarts
popsize = math.floor(
popsize0 * popsize_multiplier ** (rng.uniform() ** 2)
)
else:
poptype = "large"
n_restarts += 1
popsize = popsize0 * (inc_popsize**n_restarts)
mean = lower_bounds + (rng.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(
mean=mean,
sigma=sigma,
bounds=bounds,
seed=seed,
population_size=popsize,
)
print("Restart CMA-ES with popsize={} ({})".format(popsize, poptype))
if __name__ == "__main__":
main()
�������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/cmaes_with_margin_binary.py���������������������������������������������������0000664�0000000�0000000�00000002515�14455660762�0022116�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import CMAwM
def ellipsoid_onemax(x, n_zdim):
n = len(x)
n_rdim = n - n_zdim
r = 10
if len(x) < 2:
raise ValueError("dimension must be greater one")
ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
onemax = n_zdim - (0.0 < x[(n - n_zdim) :]).sum()
return ellipsoid + r * onemax
def main():
binary_dim, continuous_dim = 10, 10
dim = binary_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
np.tile([0, 1], (binary_dim, 1)),
]
)
steps = np.concatenate([np.zeros(continuous_dim), np.ones(binary_dim)])
optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_onemax(x_for_eval, binary_dim)
evals += 1
solutions.append((x_for_tell, value))
if evals % 300 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/cmaes_with_margin_integer.py��������������������������������������������������0000664�0000000�0000000�00000002303�14455660762�0022262�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import CMAwM
def ellipsoid_int(x, _):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
def main():
integer_dim, continuous_dim = 10, 10
dim = integer_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
np.tile([-10, 11], (integer_dim, 1)),
]
)
steps = np.concatenate([np.zeros(continuous_dim), np.ones(integer_dim)])
optimizer = CMAwM(mean=5 * np.ones(dim), sigma=2.0, bounds=bounds, steps=steps)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_int(x_for_eval, integer_dim)
evals += 1
solutions.append((x_for_tell, value))
if evals % 300 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/ellipsoid_function.py���������������������������������������������������������0000664�0000000�0000000�00000001457�14455660762�0020767�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import CMA
def ellipsoid(x):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
def main():
dim = 40
optimizer = CMA(mean=3 * np.ones(dim), sigma=2.0)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ellipsoid(x)
evals += 1
solutions.append((x, value))
if evals % 3000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/ipop_cmaes.py�����������������������������������������������������������������0000664�0000000�0000000�00000003210�14455660762�0017202�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1**2 + x2**2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e
+ 20
)
def main():
seed = 0
rng = np.random.RandomState(1)
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (rng.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
# Multiplier for increasing population size before each restart.
inc_popsize = 2
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
print(f"{generation:3d} {value:10.5f} {x[0]:6.2f} {x[1]:6.2f}")
optimizer.tell(solutions)
if optimizer.should_stop():
seed += 1
popsize = optimizer.population_size * inc_popsize
mean = lower_bounds + (rng.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(
mean=mean,
sigma=sigma,
bounds=bounds,
seed=seed,
population_size=popsize,
)
print("Restart CMA-ES with popsize={}".format(popsize))
if __name__ == "__main__":
main()
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/optuna_sampler.py�������������������������������������������������������������0000664�0000000�0000000�00000000656�14455660762�0020127�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import optuna
def objective(trial: optuna.Trial):
x1 = trial.suggest_float("x1", -4, 4)
x2 = trial.suggest_float("x2", -4, 4)
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
def main():
optuna.logging.set_verbosity(optuna.logging.INFO)
study = optuna.create_study(sampler=optuna.samplers.CmaEsSampler())
study.optimize(objective, n_trials=250, gc_after_trial=False)
if __name__ == "__main__":
main()
����������������������������������������������������������������������������������cmaes-0.10.0/examples/quadratic_function.py���������������������������������������������������������0000664�0000000�0000000�00000001345�14455660762�0020754�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import CMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
def main():
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(
f"{optimizer.generation:3d} {value:10.5f}"
f" {x[0]:6.2f} {x[1]:6.2f}"
)
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/sepcma_ellipsoid_function.py��������������������������������������������������0000664�0000000�0000000�00000001465�14455660762�0022316�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import SepCMA
def ellipsoid(x):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
def main():
dim = 40
optimizer = SepCMA(mean=3 * np.ones(dim), sigma=2.0)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ellipsoid(x)
evals += 1
solutions.append((x, value))
if evals % 3000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/examples/ws_cma_es.py������������������������������������������������������������������0000664�0000000�0000000�00000002442�14455660762�0017031�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from cmaes import CMA, get_warm_start_mgd
def source_task(x1: float, x2: float) -> float:
b = 0.4
return (x1 - b) ** 2 + (x2 - b) ** 2
def target_task(x1: float, x2: float) -> float:
b = 0.6
return (x1 - b) ** 2 + (x2 - b) ** 2
def main() -> None:
# Generate solutions from a source task
source_solutions = []
for _ in range(1000):
x = np.random.random(2)
value = source_task(x[0], x[1])
source_solutions.append((x, value))
# Estimate a promising distribution of the source task
ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(
source_solutions, gamma=0.1, alpha=0.1
)
optimizer = CMA(mean=ws_mean, sigma=ws_sigma, cov=ws_cov)
# Run WS-CMA-ES
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = target_task(x[0], x[1])
solutions.append((x, value))
print(
f"{optimizer.generation:3d} {value:10.5f}"
f" {x[0]:6.2f} {x[1]:6.2f}"
)
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/fuzzing.py�����������������������������������������������������������������������������0000664�0000000�0000000�00000002011�14455660762�0014737�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import sys
import atheris
import hypothesis.extra.numpy as npst
from hypothesis import given, strategies as st
from cmaes import CMA
@given(data=st.data())
def test_cma_tell(data):
dim = data.draw(st.integers(min_value=2, max_value=100))
mean = data.draw(npst.arrays(dtype=float, shape=dim))
sigma = data.draw(st.floats(min_value=1e-16))
n_iterations = data.draw(st.integers(min_value=1))
try:
optimizer = CMA(mean, sigma)
except AssertionError:
return
popsize = optimizer.population_size
for _ in range(n_iterations):
tell_solutions = data.draw(
st.lists(
st.tuples(npst.arrays(dtype=float, shape=dim), st.floats()),
min_size=popsize,
max_size=popsize,
)
)
optimizer.ask()
try:
optimizer.tell(tell_solutions)
except AssertionError:
return
optimizer.ask()
atheris.Setup(sys.argv, test_cma_tell.hypothesis.fuzz_one_input)
atheris.Fuzz()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/pyproject.toml�������������������������������������������������������������������������0000664�0000000�0000000�00000002574�14455660762�0015623�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������[build-system]
requires = ["setuptools>=61"]
build-backend = "setuptools.build_meta"
[project]
name = "cmaes"
description = "Lightweight Covariance Matrix Adaptation Evolution Strategy (CMA-ES) implementation for Python 3."
readme = "README.md"
authors = [
{ name = "Masashi Shibata", "email" = "m.shibata1020@gmail.com" }
]
maintainers = [
{ name = "Masahiro Nomura", "email" = "nomura_masahiro@cyberagent.co.jp" }
]
requires-python = ">=3.7"
license = {file = "LICENSE"}
classifiers = [
"Development Status :: 4 - Beta",
"Intended Audience :: Developers",
"License :: OSI Approved :: MIT License",
"Programming Language :: Python",
"Programming Language :: Python :: 3",
"Programming Language :: Python :: 3.7",
"Programming Language :: Python :: 3.8",
"Programming Language :: Python :: 3.9",
"Programming Language :: Python :: 3.10",
"Programming Language :: Python :: 3.11",
"Programming Language :: Python :: 3 :: Only",
"Intended Audience :: Science/Research",
]
dependencies = ["numpy"]
dynamic = ["version"]
[project.optional-dependencies]
cmawm = ["scipy"]
[project.urls]
"Homepage" = "https://github.com/CyberAgentAILab/cmaes"
[tool.setuptools.dynamic]
version = {attr = "cmaes.__version__"}
[tool.setuptools]
packages = ["cmaes"]
include-package-data = false
[tool.mypy]
ignore_missing_imports = true
disallow_untyped_defs = true
������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/requirements-bench.txt�����������������������������������������������������������������0000664�0000000�0000000�00000000024�14455660762�0017234�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������kurobako
cma
optuna
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/requirements-dev.txt�������������������������������������������������������������������0000664�0000000�0000000�00000000173�14455660762�0016740�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������# install_requires
numpy>=1.20.0
# visualization
matplotlib
scipy
# Fuzzing
hypothesis
atheris
# lint
mypy
flake8
black
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/setup.cfg������������������������������������������������������������������������������0000664�0000000�0000000�00000000150�14455660762�0014514�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������[flake8]
ignore =
E203,
W503
max-line-length = 100
statistics = True
exclude = venv,build,.eggs
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/setup.py�������������������������������������������������������������������������������0000664�0000000�0000000�00000000105�14455660762�0014405�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������from setuptools import setup
if __name__ == "__main__":
setup()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/���������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0014041�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/__init__.py����������������������������������������������������������������������0000664�0000000�0000000�00000000000�14455660762�0016140�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_boundary.py�����������������������������������������������������������������0000664�0000000�0000000�00000004105�14455660762�0017275�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from unittest import TestCase
from cmaes import CMA, SepCMA
CMA_CLASSES = [CMA, SepCMA]
class TestCMABoundary(TestCase):
def test_valid_dimension(self):
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
CmaClass(
mean=np.zeros(2), sigma=1.3, bounds=np.array([[-10, 10], [-10, 10]])
)
def test_invalid_dimension(self):
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
with self.assertRaises(AssertionError):
CmaClass(mean=np.zeros(2), sigma=1.3, bounds=np.array([-10, 10]))
def test_mean_located_out_of_bounds(self):
mean = np.zeros(5)
bounds = np.empty(shape=(5, 2))
bounds[:, 0], bounds[:, 1] = 1.0, 5.0
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
with self.assertRaises(AssertionError):
CmaClass(mean=mean, sigma=1.3, bounds=bounds)
def test_set_valid_bounds(self):
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
optimizer = CmaClass(mean=np.zeros(2), sigma=1.3)
optimizer.set_bounds(bounds=np.array([[-10, 10], [-10, 10]]))
def test_set_invalid_bounds(self):
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
optimizer = CmaClass(mean=np.zeros(2), sigma=1.3)
with self.assertRaises(AssertionError):
optimizer.set_bounds(bounds=np.array([-10, 10]))
def test_set_bounds_which_does_not_contain_mean(self):
for CmaClass in CMA_CLASSES:
with self.subTest(f"Class: {CmaClass.__name__}"):
optimizer = CmaClass(mean=np.zeros(2), sigma=1.3)
bounds = np.empty(shape=(5, 2))
bounds[:, 0], bounds[:, 1] = 1.0, 5.0
with self.assertRaises(AssertionError):
optimizer.set_bounds(bounds)
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_cmawm.py��������������������������������������������������������������������0000664�0000000�0000000�00000002315�14455660762�0016557�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import warnings
import numpy as np
from numpy.testing import assert_almost_equal
from unittest import TestCase
from cmaes import CMA, CMAwM
class TestCMAwM(TestCase):
def test_no_discrete_spaces(self):
mean = np.zeros(2)
bounds = np.array([[-10, 10], [-10, 10]])
steps = np.array([0, 0])
sigma = 1.3
seed = 1
cma_optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=seed)
with warnings.catch_warnings():
warnings.simplefilter("ignore", category=UserWarning)
cmawm_optimizer = CMAwM(
mean=mean, sigma=sigma, bounds=bounds, steps=steps, seed=seed
)
for i in range(100):
solutions = []
for _ in range(cma_optimizer.population_size):
cma_x = cma_optimizer.ask()
cmawm_x_encoded, cmawm_x_for_tell = cmawm_optimizer.ask()
assert_almost_equal(cma_x, cmawm_x_encoded)
assert_almost_equal(cma_x, cmawm_x_for_tell)
objective = (cma_x[0] - 3) ** 2 + cma_x[1] ** 2
solutions.append((cma_x, objective))
cma_optimizer.tell(solutions)
cmawm_optimizer.tell(solutions)
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_compress_symmetric.py�������������������������������������������������������0000664�0000000�0000000�00000002161�14455660762�0021401�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from unittest import TestCase
from cmaes._cma import _decompress_symmetric, _compress_symmetric
class TestCompressSymmetric(TestCase):
def test_compress_symmetric_odd(self):
sym2d = np.array([[1, 2], [2, 3]])
actual = _compress_symmetric(sym2d)
expected = np.array([1, 2, 3])
self.assertTrue(np.all(np.equal(actual, expected)))
def test_compress_symmetric_even(self):
sym2d = np.array([[1, 2, 3], [2, 4, 5], [3, 5, 6]])
actual = _compress_symmetric(sym2d)
expected = np.array([1, 2, 3, 4, 5, 6])
self.assertTrue(np.all(np.equal(actual, expected)))
def test_decompress_symmetric_odd(self):
sym1d = np.array([1, 2, 3])
actual = _decompress_symmetric(sym1d)
expected = np.array([[1, 2], [2, 3]])
self.assertTrue(np.all(np.equal(actual, expected)))
def test_decompress_symmetric_even(self):
sym1d = np.array([1, 2, 3, 4, 5, 6])
actual = _decompress_symmetric(sym1d)
expected = np.array([[1, 2, 3], [2, 4, 5], [3, 5, 6]])
self.assertTrue(np.all(np.equal(actual, expected)))
���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_fuzzing.py������������������������������������������������������������������0000664�0000000�0000000�00000004003�14455660762�0017143�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import hypothesis.extra.numpy as npst
import unittest
from hypothesis import given, strategies as st
from cmaes import CMA, SepCMA
class TestFuzzing(unittest.TestCase):
@given(
data=st.data(),
)
def test_cma_tell(self, data):
dim = data.draw(st.integers(min_value=2, max_value=100))
mean = data.draw(npst.arrays(dtype=float, shape=dim))
sigma = data.draw(st.floats(min_value=1e-16))
n_iterations = data.draw(st.integers(min_value=1))
try:
optimizer = CMA(mean, sigma)
except AssertionError:
return
popsize = optimizer.population_size
for _ in range(n_iterations):
tell_solutions = data.draw(
st.lists(
st.tuples(npst.arrays(dtype=float, shape=dim), st.floats()),
min_size=popsize,
max_size=popsize,
)
)
optimizer.ask()
try:
optimizer.tell(tell_solutions)
except AssertionError:
return
optimizer.ask()
@given(
data=st.data(),
)
def test_sepcma_tell(self, data):
dim = data.draw(st.integers(min_value=2, max_value=100))
mean = data.draw(npst.arrays(dtype=float, shape=dim))
sigma = data.draw(st.floats(min_value=1e-16))
n_iterations = data.draw(st.integers(min_value=1))
try:
optimizer = SepCMA(mean, sigma)
except AssertionError:
return
popsize = optimizer.population_size
for _ in range(n_iterations):
tell_solutions = data.draw(
st.lists(
st.tuples(npst.arrays(dtype=float, shape=dim), st.floats()),
min_size=popsize,
max_size=popsize,
)
)
optimizer.ask()
try:
optimizer.tell(tell_solutions)
except AssertionError:
return
optimizer.ask()
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_stats.py��������������������������������������������������������������������0000664�0000000�0000000�00000002716�14455660762�0016616�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import math
from unittest import TestCase
from cmaes import _stats
# Test Cases in this file is generated by SciPy v1.9.3
class TestNormCDF(TestCase):
def test_standard_normal_distribution(self):
self.assertAlmostEqual(_stats.norm_cdf(-30), 4.906713927147907e-198, places=205)
self.assertAlmostEqual(_stats.norm_cdf(-10), 7.619853024160469e-24, places=30)
self.assertAlmostEqual(_stats.norm_cdf(-1), 0.15865525393145707)
self.assertAlmostEqual(_stats.norm_cdf(0), 0.5)
self.assertAlmostEqual(_stats.norm_cdf(1), 0.8413447460685429)
self.assertAlmostEqual(
_stats.norm_cdf(8),
0.9999999999999993338661852249060757458209991455078125,
places=30,
)
self.assertAlmostEqual(_stats.norm_cdf(10), 1.0)
def test_mu_and_sigma(self):
self.assertAlmostEqual(_stats.norm_cdf(1, loc=2, scale=3), 0.36944134018176367)
class TestChi2PPF(TestCase):
def test(self):
self.assertAlmostEqual(_stats.chi2_ppf(0.0), 0.0)
self.assertAlmostEqual(
_stats.chi2_ppf(0.00000001), 1.5707963267948962e-16, places=25
)
self.assertAlmostEqual(_stats.chi2_ppf(0.5), 0.454936423119572)
self.assertAlmostEqual(_stats.chi2_ppf(0.99999999), 32.84125335146885)
self.assertAlmostEqual(
_stats.chi2_ppf(0.999999999999999777955395074969), 67.39648382445012
)
self.assertAlmostEqual(_stats.chi2_ppf(1.0), math.inf)
��������������������������������������������������cmaes-0.10.0/tests/test_termination_criterion.py����������������������������������������������������0000664�0000000�0000000�00000001612�14455660762�0022061�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from unittest import TestCase
from cmaes import CMA
class TestTerminationCriterion(TestCase):
def test_stop_if_objective_values_are_not_changed(self):
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
popsize = optimizer.population_size
rng = np.random.RandomState(seed=1)
for i in range(optimizer._funhist_term + 1):
self.assertFalse(optimizer.should_stop())
optimizer.tell([(rng.randn(2), 0.01) for _ in range(popsize)])
self.assertTrue(optimizer.should_stop())
def test_stop_if_detect_divergent_behavior(self):
optimizer = CMA(mean=np.zeros(2), sigma=1e-4)
popsize = optimizer.population_size
nd_rng = np.random.RandomState(1)
solutions = [(100 * nd_rng.randn(2), 0.01) for _ in range(popsize)]
optimizer.tell(solutions)
self.assertTrue(optimizer.should_stop())
����������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tests/test_warm_start.py���������������������������������������������������������������0000664�0000000�0000000�00000000620�14455660762�0017633�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import numpy as np
from unittest import TestCase
from cmaes import CMA, get_warm_start_mgd
class TestWarmStartCMA(TestCase):
def test_dimension(self):
optimizer = CMA(mean=np.zeros(10), sigma=1.3)
source_solutions = [(optimizer.ask(), 0.0) for _ in range(100)]
ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(source_solutions)
self.assertEqual(ws_mean.size, 10)
����������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tools/���������������������������������������������������������������������������������0000775�0000000�0000000�00000000000�14455660762�0014037�5����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tools/cmaes_visualizer.py��������������������������������������������������������������0000664�0000000�0000000�00000020035�14455660762�0017756�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������"""
Usage:
cmaes_visualizer.py OPTIONS
Optional arguments:
-h, --help show this help message and exit
--function {quadratic,himmelblau,rosenbrock,six-hump-camel}
--seed SEED
--frames FRAMES
--interval INTERVAL
--pop-per-frame POP_PER_FRAME
--restart-strategy {ipop,bipop}
Example:
python3 cmaes_visualizer.py --function six-hump-camel --pop-per-frame 2
python3 tools/cmaes_visualizer.py --function himmelblau \
--restart-strategy ipop --frames 500 --interval 10 --pop-per-frame 6
"""
import argparse
import math
import numpy as np
from scipy import stats
from matplotlib.colors import LinearSegmentedColormap
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from pylab import rcParams
from cmaes._cma import CMA
parser = argparse.ArgumentParser()
parser.add_argument(
"--function",
choices=["quadratic", "himmelblau", "rosenbrock", "six-hump-camel"],
)
parser.add_argument(
"--seed",
type=int,
default=1,
)
parser.add_argument(
"--frames",
type=int,
default=100,
)
parser.add_argument(
"--interval",
type=int,
default=20,
)
parser.add_argument(
"--pop-per-frame",
type=int,
default=1,
)
parser.add_argument(
"--restart-strategy",
choices=["ipop", "bipop"],
default="",
)
args = parser.parse_args()
rcParams["figure.figsize"] = 10, 5
fig, (ax1, ax2) = plt.subplots(1, 2)
color_dict = {
"red": ((0.0, 0.0, 0.0), (1.0, 1.0, 1.0)),
"green": ((0.0, 0.0, 0.0), (1.0, 1.0, 1.0)),
"blue": ((0.0, 1.0, 1.0), (1.0, 1.0, 1.0)),
"yellow": ((1.0, 1.0, 1.0), (1.0, 1.0, 1.0)),
}
bw = LinearSegmentedColormap("BlueWhile", color_dict)
def himmelbleu(x1, x2):
return (x1**2 + x2 - 11.0) ** 2 + (x1 + x2**2 - 7.0) ** 2
def himmelbleu_contour(x1, x2):
return np.log(himmelbleu(x1, x2) + 1)
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
def quadratic_contour(x1, x2):
return np.log(quadratic(x1, x2) + 1)
def rosenbrock(x1, x2):
return 100 * (x2 - x1**2) ** 2 + (x1 - 1) ** 2
def rosenbrock_contour(x1, x2):
return np.log(rosenbrock(x1, x2) + 1)
def six_hump_camel(x1, x2):
return (
(4 - 2.1 * (x1**2) + (x1**4) / 3) * (x1**2)
+ x1 * x2
+ (-4 + 4 * x2**2) * (x2**2)
)
def six_hump_camel_contour(x1, x2):
return np.log(six_hump_camel(x1, x2) + 1.0316)
function_name = ""
if args.function == "quadratic":
function_name = "Quadratic function"
objective = quadratic
contour_function = quadratic_contour
global_minimums = [
(3.0, -2.0),
]
# input domain
x1_lower_bound, x1_upper_bound = -4, 4
x2_lower_bound, x2_upper_bound = -4, 4
elif args.function == "himmelblau":
function_name = "Himmelblau function"
objective = himmelbleu
contour_function = himmelbleu_contour
global_minimums = [
(3.0, 2.0),
(-2.805118, 3.131312),
(-3.779310, -3.283186),
(3.584428, -1.848126),
]
# input domain
x1_lower_bound, x1_upper_bound = -4, 4
x2_lower_bound, x2_upper_bound = -4, 4
elif args.function == "rosenbrock":
# https://www.sfu.ca/~ssurjano/rosen.html
function_name = "Rosenbrock function"
objective = rosenbrock
contour_function = rosenbrock_contour
global_minimums = [
(1, 1),
]
# input domain
x1_lower_bound, x1_upper_bound = -5, 10
x2_lower_bound, x2_upper_bound = -5, 10
elif args.function == "six-hump-camel":
# https://www.sfu.ca/~ssurjano/camel6.html
function_name = "Six-hump camel function"
objective = six_hump_camel
contour_function = six_hump_camel_contour
global_minimums = [
(0.0898, -0.7126),
(-0.0898, 0.7126),
]
# input domain
x1_lower_bound, x1_upper_bound = -3, 3
x2_lower_bound, x2_upper_bound = -2, 2
else:
raise ValueError("invalid function type")
seed = args.seed
bounds = np.array([[x1_lower_bound, x1_upper_bound], [x2_lower_bound, x2_upper_bound]])
sigma = (x1_upper_bound - x2_lower_bound) / 5
optimizer = CMA(mean=np.zeros(2), sigma=sigma, bounds=bounds, seed=seed)
solutions = []
trial_number = 0
rng = np.random.RandomState(seed)
# Variables for IPOP and BIPOP
inc_popsize = 2
n_restarts = 0 # A small restart doesn't count in the n_restarts
small_n_eval, large_n_eval = 0, 0
popsize0 = optimizer.population_size
poptype = "small"
def init():
ax1.set_xlim(x1_lower_bound, x1_upper_bound)
ax1.set_ylim(x2_lower_bound, x2_upper_bound)
ax2.set_xlim(x1_lower_bound, x1_upper_bound)
ax2.set_ylim(x2_lower_bound, x2_upper_bound)
# Plot 4 local minimum value
for m in global_minimums:
ax1.plot(m[0], m[1], "y*", ms=10)
ax2.plot(m[0], m[1], "y*", ms=10)
# Plot contour of himmelbleu function
x1 = np.arange(x1_lower_bound, x1_upper_bound, 0.01)
x2 = np.arange(x2_lower_bound, x2_upper_bound, 0.01)
x1, x2 = np.meshgrid(x1, x2)
ax1.contour(x1, x2, contour_function(x1, x2), 30, cmap=bw)
def get_next_popsize():
global optimizer, n_restarts, poptype, small_n_eval, large_n_eval
if args.restart_strategy == "ipop":
n_restarts += 1
popsize = optimizer.population_size * inc_popsize
print(f"Restart CMA-ES with popsize={popsize} at trial={trial_number}")
return popsize
elif args.restart_strategy == "bipop":
n_eval = optimizer.population_size * optimizer.generation
if poptype == "small":
small_n_eval += n_eval
else: # poptype == "large"
large_n_eval += n_eval
if small_n_eval < large_n_eval:
poptype = "small"
popsize_multiplier = inc_popsize**n_restarts
popsize = math.floor(popsize0 * popsize_multiplier ** (rng.uniform() ** 2))
else:
poptype = "large"
n_restarts += 1
popsize = popsize0 * (inc_popsize**n_restarts)
print(
f"Restart CMA-ES with popsize={popsize} ({poptype}) at trial={trial_number}"
)
return
raise Exception("must not reach here")
def update(frame):
global solutions, optimizer, trial_number
if len(solutions) == optimizer.population_size:
optimizer.tell(solutions)
solutions = []
if optimizer.should_stop():
popsize = get_next_popsize()
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (rng.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(
mean=mean,
sigma=sigma,
bounds=bounds,
seed=seed,
population_size=popsize,
)
n_sample = min(optimizer.population_size - len(solutions), args.pop_per_frame)
for i in range(n_sample):
x = optimizer.ask()
evaluation = objective(x[0], x[1])
# Plot sample points
ax1.plot(x[0], x[1], "o", c="r", label="2d", alpha=0.5)
solution = (
x,
evaluation,
)
solutions.append(solution)
trial_number += n_sample
# Update title
if args.restart_strategy == "ipop":
fig.suptitle(
f"IPOP-CMA-ES {function_name} trial={trial_number} "
f"popsize={optimizer.population_size}"
)
elif args.restart_strategy == "bipop":
fig.suptitle(
f"BIPOP-CMA-ES {function_name} trial={trial_number} "
f"popsize={optimizer.population_size} ({poptype})"
)
else:
fig.suptitle(f"CMA-ES {function_name} trial={trial_number}")
# Plot multivariate gaussian distribution of CMA-ES
x, y = np.mgrid[
x1_lower_bound:x1_upper_bound:0.01, x2_lower_bound:x2_upper_bound:0.01
]
rv = stats.multivariate_normal(optimizer._mean, optimizer._C)
pos = np.dstack((x, y))
ax2.contourf(x, y, rv.pdf(pos))
if frame % 50 == 0:
print(f"Processing frame {frame}")
def main():
ani = animation.FuncAnimation(
fig,
update,
frames=args.frames,
init_func=init,
blit=False,
interval=args.interval,
)
ani.save(f"./tmp/{args.function}.mp4")
if __name__ == "__main__":
main()
���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tools/optuna_profile.py����������������������������������������������������������������0000664�0000000�0000000�00000002117�14455660762�0017440�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������import argparse
import cProfile
import logging
import pstats
import optuna
parser = argparse.ArgumentParser()
parser.add_argument("--storage", choices=["memory", "sqlite"], default="memory")
parser.add_argument("--params", type=int, default=100)
parser.add_argument("--trials", type=int, default=1000)
args = parser.parse_args()
def objective(trial: optuna.Trial):
val = 0
for i in range(args.params):
xi = trial.suggest_uniform(str(i), -4, 4)
val += (xi - 2) ** 2
return val
def main():
logging.disable(level=logging.INFO)
storage = None
if args.storage == "sqlite":
storage = f"sqlite:///db-{args.trials}-{args.params}.sqlite3"
sampler = optuna.samplers.CmaEsSampler()
study = optuna.create_study(sampler=sampler, storage=storage)
profiler = cProfile.Profile()
profiler.runcall(
study.optimize, objective, n_trials=args.trials, gc_after_trial=False
)
profiler.dump_stats("profile.stats")
stats = pstats.Stats("profile.stats")
stats.sort_stats("time").print_stats(5)
if __name__ == "__main__":
main()
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������cmaes-0.10.0/tools/ws_cmaes_visualizer.py�����������������������������������������������������������0000664�0000000�0000000�00000016004�14455660762�0020470�0����������������������������������������������������������������������������������������������������ustar�00root����������������������������root����������������������������0000000�0000000������������������������������������������������������������������������������������������������������������������������������������������������������������������������"""
Usage:
python3 tools/ws_cmaes_visualizer.py OPTIONS
Optional arguments:
-h, --help show this help message and exit
--function {quadratic,himmelblau,rosenbrock,six-hump-camel,sphere,rot-ellipsoid}
--seed SEED
--alpha ALPHA
--gamma GAMMA
--frames FRAMES
--interval INTERVAL
--pop-per-frame POP_PER_FRAME
Example:
python3 ws_cmaes_visualizer.py --function rot-ellipsoid
"""
import argparse
import math
import numpy as np
from scipy import stats
from matplotlib.colors import LinearSegmentedColormap
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from pylab import rcParams
from cmaes import get_warm_start_mgd
parser = argparse.ArgumentParser()
parser.add_argument(
"--function",
choices=[
"quadratic",
"himmelblau",
"rosenbrock",
"six-hump-camel",
"sphere",
"rot-ellipsoid",
],
)
parser.add_argument(
"--seed",
type=int,
default=1,
)
parser.add_argument(
"--alpha",
type=float,
default=0.1,
)
parser.add_argument(
"--gamma",
type=float,
default=0.1,
)
parser.add_argument(
"--frames",
type=int,
default=100,
)
parser.add_argument(
"--interval",
type=int,
default=20,
)
parser.add_argument(
"--pop-per-frame",
type=int,
default=10,
)
args = parser.parse_args()
rcParams["figure.figsize"] = 10, 5
fig, (ax1, ax2) = plt.subplots(1, 2)
color_dict = {
"red": ((0.0, 0.0, 0.0), (1.0, 1.0, 1.0)),
"green": ((0.0, 0.0, 0.0), (1.0, 1.0, 1.0)),
"blue": ((0.0, 1.0, 1.0), (1.0, 1.0, 1.0)),
"yellow": ((1.0, 1.0, 1.0), (1.0, 1.0, 1.0)),
}
bw = LinearSegmentedColormap("BlueWhile", color_dict)
def himmelbleu(x1, x2):
return (x1**2 + x2 - 11.0) ** 2 + (x1 + x2**2 - 7.0) ** 2
def himmelbleu_contour(x1, x2):
return np.log(himmelbleu(x1, x2) + 1)
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
def quadratic_contour(x1, x2):
return np.log(quadratic(x1, x2) + 1)
def rosenbrock(x1, x2):
return 100 * (x2 - x1**2) ** 2 + (x1 - 1) ** 2
def rosenbrock_contour(x1, x2):
return np.log(rosenbrock(x1, x2) + 1)
def six_hump_camel(x1, x2):
return (
(4 - 2.1 * (x1**2) + (x1**4) / 3) * (x1**2)
+ x1 * x2
+ (-4 + 4 * x2**2) * (x2**2)
)
def six_hump_camel_contour(x1, x2):
return np.log(six_hump_camel(x1, x2) + 1.0316)
def sphere(x1, x2):
offset = 0.6
return (x1 - offset) ** 2 + (x2 - offset) ** 2
def sphere_contour(x1, x2):
return np.log(sphere(x1, x2) + 1)
def ellipsoid(x1, x2):
offset = 0.6
scale = 5**2
return (x1 - offset) ** 2 + scale * (x2 - offset) ** 2
def rot_ellipsoid(x1, x2):
rot_x1 = math.sqrt(3.0) / 2.0 * x1 + 1.0 / 2.0 * x2
rot_x2 = 1.0 / 2.0 * x1 + math.sqrt(3.0) / 2.0 * x2
return ellipsoid(rot_x1, rot_x2)
def rot_ellipsoid_contour(x1, x2):
return np.log(rot_ellipsoid(x1, x2) + 1)
function_name = ""
if args.function == "quadratic":
function_name = "Quadratic function"
objective = quadratic
contour_function = quadratic_contour
global_minimums = [
(3.0, -2.0),
]
# input domain
x1_lower_bound, x1_upper_bound = -4, 4
x2_lower_bound, x2_upper_bound = -4, 4
elif args.function == "himmelblau":
function_name = "Himmelblau function"
objective = himmelbleu
contour_function = himmelbleu_contour
global_minimums = [
(3.0, 2.0),
(-2.805118, 3.131312),
(-3.779310, -3.283186),
(3.584428, -1.848126),
]
# input domain
x1_lower_bound, x1_upper_bound = -4, 4
x2_lower_bound, x2_upper_bound = -4, 4
elif args.function == "rosenbrock":
# https://www.sfu.ca/~ssurjano/rosen.html
function_name = "Rosenbrock function"
objective = rosenbrock
contour_function = rosenbrock_contour
global_minimums = [
(1, 1),
]
# input domain
x1_lower_bound, x1_upper_bound = -5, 10
x2_lower_bound, x2_upper_bound = -5, 10
elif args.function == "six-hump-camel":
# https://www.sfu.ca/~ssurjano/camel6.html
function_name = "Six-hump camel function"
objective = six_hump_camel
contour_function = six_hump_camel_contour
global_minimums = [
(0.0898, -0.7126),
(-0.0898, 0.7126),
]
# input domain
x1_lower_bound, x1_upper_bound = -3, 3
x2_lower_bound, x2_upper_bound = -2, 2
elif args.function == "sphere":
function_name = "Sphere function with offset=0.6"
objective = sphere
contour_function = sphere_contour
global_minimums = [
(0.6, 0.6),
]
# input domain
x1_lower_bound, x1_upper_bound = 0, 1
x2_lower_bound, x2_upper_bound = 0, 1
elif args.function == "rot-ellipsoid":
function_name = "Rot Ellipsoid function with offset=0.6"
objective = rot_ellipsoid
contour_function = rot_ellipsoid_contour
global_minimums = []
# input domain
x1_lower_bound, x1_upper_bound = 0, 1
x2_lower_bound, x2_upper_bound = 0, 1
else:
raise ValueError("invalid function type")
seed = args.seed
rng = np.random.RandomState(seed)
solutions = []
def init():
ax1.set_xlim(x1_lower_bound, x1_upper_bound)
ax1.set_ylim(x2_lower_bound, x2_upper_bound)
ax2.set_xlim(x1_lower_bound, x1_upper_bound)
ax2.set_ylim(x2_lower_bound, x2_upper_bound)
# Plot 4 local minimum value
for m in global_minimums:
ax1.plot(m[0], m[1], "y*", ms=10)
ax2.plot(m[0], m[1], "y*", ms=10)
# Plot contour of the function
x1 = np.arange(x1_lower_bound, x1_upper_bound, 0.01)
x2 = np.arange(x2_lower_bound, x2_upper_bound, 0.01)
x1, x2 = np.meshgrid(x1, x2)
ax1.contour(x1, x2, contour_function(x1, x2), 30, cmap=bw)
def update(frame):
global solutions
for i in range(args.pop_per_frame):
x1 = (x1_upper_bound - x1_lower_bound) * rng.random() + x1_lower_bound
x2 = (x2_upper_bound - x2_lower_bound) * rng.random() + x2_lower_bound
evaluation = objective(x1, x2)
# Plot sample points
ax1.plot(x1, x2, "o", c="r", label="2d", alpha=0.5)
solution = (
np.array([x1, x2], dtype=float),
evaluation,
)
solutions.append(solution)
# Update title
fig.suptitle(
f"WS-CMA-ES {function_name} with alpha={args.alpha} and gamma={args.gamma} (frame={frame})"
)
# Plot multivariate gaussian distribution of CMA-ES
x, y = np.mgrid[
x1_lower_bound:x1_upper_bound:0.01, x2_lower_bound:x2_upper_bound:0.01
]
if math.floor(len(solutions) * args.alpha) > 1:
mean, sigma, cov = get_warm_start_mgd(
solutions, alpha=args.alpha, gamma=args.gamma
)
rv = stats.multivariate_normal(mean, cov)
pos = np.dstack((x, y))
ax2.contourf(x, y, rv.pdf(pos))
if frame % 50 == 0:
print(f"Processing frame {frame}")
def main():
ani = animation.FuncAnimation(
fig,
update,
frames=args.frames,
init_func=init,
blit=False,
interval=args.interval,
)
ani.save(f"./tmp/{args.function}.mp4")
if __name__ == "__main__":
main()
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������